GLU 和 SwiGLU#
PaLM 和 LLaMA 中都使用 SwiGLU 替换了 FFN,本文介绍一下 GLU 和 SwiGLU。
GLU论文链接: https://arxiv.org/pdf/1612.08083.pdf
SwiGLU论文链接: https://arxiv.org/pdf/2002.05202.pdf
PaLM论文链接: https://arxiv.org/pdf/2204.02311.pdf
LLaMA论文链接: https://arxiv.org/pdf/2302.13971.pdf
关于符号的说明:本文对应着两篇论文,一篇是GLU,另一篇是SwiGLU。在下文中描述GLU和SwiGLU时各自使用对应论文中的符号,所以有可能出现符号不一致的问题。
1、GLU#
出自2017年的论文 Language Modeling with Gated Convolutional Networks
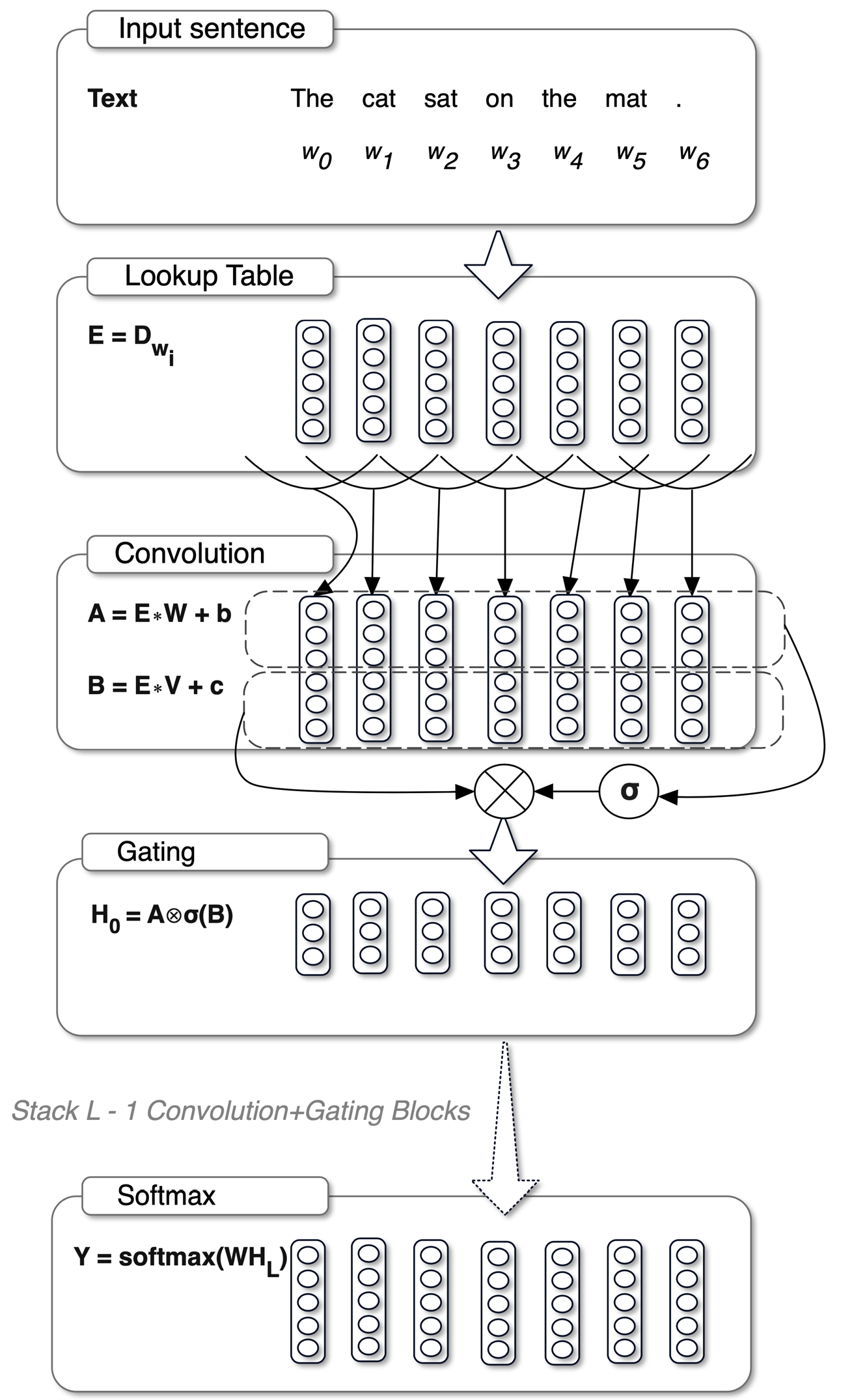
GLU 全称为 Gated Linear Unit,即门控线性单元函数。在原始论文中使用下图1来解释该函数,下图是一个完整的网络结构,其中 "Input Sentence"、"Lookup Table" 都是输入层,"Softmax" 是输出层,这两部分都不考虑。接下来主要看的是下图的 "Convolution" 和 "Gating" 这两层,这两层对应的就是 GLU。
首先输入向量x(在下图中使用的符号是E)经过两个独立的卷积层/MLP层,得到向量A和向量B。此时,向量A和向量B的公式为:A=x \cdot W + b,B=x \cdot V + c。然后向量B经过一个sigmoid函数之后,\sigma(B)中的每个元素就都变为了0~1之间的值,就可以起到控制信息是否通过的作用(下图画的是向量A经过sigmoid函数,这是有点问题的)。
将向量A与\sigma(B)逐个元素相乘之后就得到了GLU层的最终输出结果,把上面描述的整个过程结合起来,GLU的公式如下:
在该公式中,x 表示输入向量,\otimes 表示两个向量逐元素相乘,\sigma 表示sigmoid函数。
| 图1 |
|---|
 |
公式(1)是原论文中提出的公式形式,当GLU作为激活函数时一般不是上述公式(1)的形式。激活函数 ReLU 的公式为 \text{ReLU} = \max(0, x),其含义就是当输入向量 x 的值小于 0 时直接阻断,当时输入向量 x 的值大于 0 值直接通过。参考ReLU激活函数,激活函数GLU的公式为如下公式(2)的形式:
这里有一个新符号 g(x) 表示的是向量 x 经过一层MLP或者卷积层,其他部分的符号与公式(1)中是相同的。可以看出公式(2)的右半部分与公式(1)的右半部分是完全一样的,所不同的是公式(2)中的左半部分直接就是向量 x,这和上面描述的激活函数ReLU是相似的,当 \sigma(g(x)) 趋近于 0 时表示对 x 进行阻断,当 \sigma(g(x)) 趋近于 1 时表示允许 x 通过,以此实现门控激活函数的效果。
2、SwiGLU#
2.1 FFN公式及其变体#
我们知道FFN就是输入向量x先经过一个MLP层,将维度上升到原来的4倍,然后过一个激活函数层,最后再经过一个MLP层,将维度还原回去。其公式为:
有些研究,比如T5,将实验中的偏置项去掉了,这样FFN就变为了如下形式:
把这里的激活函数由 ReLU 替换为 GeLU 或 Swish 之后,就得到两种新的FFN,公式如下,下面这两种也都有相应的实验结果。
从这里来看,深度学习还是穷举各种情况挨个试一遍:ReLU、GeLU、Swish,以及本文的 GLU。
2.2 GLU公式及其变体#
上一小节中的公式(1)为原始的 GLU 公式,在这里我们重新写一遍,如下:
在该公式中,左侧部分有一个Sigmoid函数,把这个函数替换为其他函数就可以得到GLU函数的各种变体,下面是其一系列变体。公式(8)是直接把Sigmoid函数去掉,公式(9)、(10)、(11)是分别把Sigmoid函数替换为ReLU、GeLU、Swish:
接下来把所有的偏置项都给去掉,就得到下述五个公式,大同小异没什么本质区别:
2.3 将FFN的变体与GLU的变体结合#
使用公式(12)中的 GLU 及其各种变体替换掉 FFN 中的第一个MLP和激活函数,就可以得到如下新版的 FFN 公式:
接下来就是做实验验证上述各个新版的FFN与原版的FFN究竟哪个效果更好了。就目前来看,PaLM 和 LLaMA 中都是使用的 \text{FFN}_{\text{SwiGLU}}。
2.4 SwiGLU替换之后的维度#
原来的FFN有两个MLP层,这两个MLP层的参数量分别为:h \times 4h 和 4h \times h,总的参数量为 8h^2。
SwiGLU 的公式为:
从上述公式中可以知道,矩阵 W 与矩阵 V 的维度是相同的,其作用是对输入向量 x 进行升维;矩阵 W_2 的作用是将高维的隐向量还原到和输入向量 x 相同的维度。所以 W、V、W_2 这三个矩阵的维度分别为:(h, \alpha h)、(h, \alpha h)、(\alpha h, h),总的参数量为 3\alpha h^2。为了保持和原始的 FFN 参数量相同,有:
解得 \alpha=\frac{8}{3},最终 W、V、W_2 这三个矩阵的维度分别为:(h, \frac{8}{3} h)、(h, \frac{8}{3} h)、(\frac{8}{3} h, h),可以很明显的看出严格按照该公式计算出来的不是整数,所以使用该公式计算出来的是模型真实维度的近似值。
下面是65B的LLaMA的模型结构,可以看到在attention部分隐藏层的维度为8192,乘上 \frac{8}{3} 就是 8192 * \frac{8}{3} = 21845.33,与下述模型中真实的维度 22016 是基本一致的。
LlamaForCausalLM(
(model): LlamaModel(
(embed_tokens): Embedding(32000, 8192, padding_idx=0)
(layers): ModuleList(
(0-79): 80 x LlamaDecoderLayer(
(self_attn): LlamaAttention(
(q_proj): Linear4bit(in_features=8192, out_features=8192, bias=False)
(k_proj): Linear4bit(in_features=8192, out_features=8192, bias=False)
(v_proj): Linear4bit(in_features=8192, out_features=8192, bias=False)
(o_proj): Linear4bit(in_features=8192, out_features=8192, bias=False)
(rotary_emb): LlamaRotaryEmbedding()
)
(mlp): LlamaMLP(
(gate_proj): Linear4bit(in_features=8192, out_features=22016, bias=False)
(down_proj): Linear4bit(in_features=22016, out_features=8192, bias=False)
(up_proj): Linear4bit(in_features=8192, out_features=22016, bias=False)
(act_fn): SiLUActivation()
)
(input_layernorm): LlamaRMSNorm()
(post_attention_layernorm): LlamaRMSNorm()
)
)
(norm): LlamaRMSNorm()
)
(lm_head): Linear(in_features=8192, out_features=32000, bias=False)
)