[隐藏左侧目录栏][显示左侧目录栏]

Proximal Policy Optimization#

上一节介绍的 Policy Gradient 是 on-policy 的方法，这种方法的缺陷是数据的利用率太低，花了很大的时间采样到一批数据之后只用于更新一次梯度，然后就要再次采样数据了。其梯度求解公式如下所示：

\begin{equation}\nabla \bar{R}_{\theta} = E_{\tau \backsim p_{\theta}(\tau)} \Big[ \sum_{t=1}^T R(\tau) \cdot \nabla \text{log} p_{\theta}(a_t|s_t) \Big]\end{equation}

接下来要介绍的 Proximal Policy Optimization（PPO）方法是使用参数为 \theta^\prime 的 model 与环境进行交互采样数据，然后使用这批数据对参数为 \theta 的 model 进行参数的更新，并且采样到的数据可以使用多次。这里在刚看的时候有一个疑问，就是：如果使用另外一个模型采样的数据可以使用多次，为什么直接使用参数为 \theta 的 model 采样到的数据不能够使用多次。这里的原因主要是：使用参数为 \theta^\prime 的 model 采样的数据并不是直接用来对参数为 \theta 的 model 进行更新（因为本身这两个 model 所对应的分布就不一样，直接使用就是错误的），而是在对参数为 \theta 的 model 进行更新时是有一个 "修正" 的。这个所谓的 "修正" 使用到的理论工具就是 Important Sampling。

1、Important Sampling#

1.1 基础理论#

如果要求解期望 E_{x \backsim p(x)} [f(x)] 可以使用如下公式进行求解：

\begin{equation}E_{x \backsim p(x)} [f(x)] = \int p(x) \cdot f(x) \text{d}x\end{equation}

如果积分求解比较困难，或者积分无法求解，还可以使用下式对期望 E_{x \backsim p(x)} [f(x)] 进行近似求解。该公式中 x^{(i)} 是从分布 p(x) 中采样的样本，随着采样的样本数量 N 越大，那么下述公式计算出的值就越接近真实期望值。

\begin{equation}E_{x \backsim p(x)} [f(x)] \approx \frac{1}{N}\sum_{i=1}^N f(x^{(i)})\end{equation}

更进一步的，如果要求解期望 E_{x \backsim p(x)} [f(x)] 时，不仅积分无法求解，分布 p(x) 也由于某些原因无法进行采样样本。那么还可以借助一个任意的可进行采样的分布 q(x) 来近似求解该期望值。公式推导过程如下所示：

\begin{equation}\begin{split} E_{x \backsim p(x)} [f(x)] &= \int p(x) \cdot f(x) \text{d}x \\ &= \int q(x) \cdot f(x)\frac{p(x)}{q(x)} \text{d}x \\ &= E_{x \backsim q(x)} \Big[ f(x)\frac{p(x)}{q(x)} \Big] \end{split}\end{equation}

在上述公式（4）的最后一行中的 x 就是从分布 q(x) 中采样出来的样本。并且，从上述推导过程中可以看出，对分布 q(x) 的限制只有其作为分母不能为0的限制，没有其他的任何限制，其可以选用任何分布。

1.2 实际使用时该方法的局限性#

虽然上面已经说过从理论上来看，分布 q(x) 可以是任意的分布，但是在实际使用时，分布 q(x) 还是需要尽量与分布 p(x) 接近比较好，否则训练起来就会非常困难，下面说明一下为什么需要分布 q(x) 与分布 p(x) 比较接近。

由上面的分析可知期望 E_{x \backsim p(x)}[f(x)] 与期望 E_{x \backsim q(x)}[f(x)\frac{p(x)}{q(x)}] 是相同的，即有下式成立：

\begin{equation}E_{x \backsim p(x)}[f(x)]=E_{x \backsim q(x)}[f(x)\frac{p(x)}{q(x)}]\end{equation}

然后分析一下方差 Var_{x \backsim p(x)}[f(x)] 和方差 Var_{x \backsim q(x)}[f(x)\frac{p(x)}{q(x)}] 是否相同，先对这两个方差进行变形和化简，如下：

这里求解方差使用到了公式：Var[X] = E[X^2] - (E[X])^2

\begin{equation}Var_{x \backsim p(x)}[f(x)] = E_{x \backsim p(x)}\Big[ (f(x))^2 \Big] - \Big(E_{x \backsim p(x) }\big[f(x)\big] \Big)^2\end{equation}
\begin{equation}\begin{split} Var_{x \backsim q(x)}[f(x)\frac{p(x)}{q(x)}] &= E_{x \backsim q(x)}\Big[ \big(f(x) \frac{p(x)}{q(x)} \big)^2\Big] - \Big(E_{x \backsim q(x) }\big[f(x)\frac{p(x)}{q(x)}\big] \Big)^2 \\ &= \int q(x) \cdot \Big(f(x) \frac{p(x)}{q(x)} \Big)^2 \text{d}x - \Big(E_{x \backsim p(x) }\big[f(x)\big] \Big)^2 \\ &= \int p(x) \cdot \big(f(x)\big)^2 \frac{p(x)}{q(x)} \text{d}x - \Big(E_{x \backsim p(x) }\big[f(x)\big] \Big)^2 \\ &= E_{x \backsim p(x)} \Big[ \big(f(x)\big)^2 \frac{p(x)}{q(x)} \Big] - \Big(E_{x \backsim p(x) }\big[f(x)\big] \Big)^2 \end{split}\end{equation}

对比公式（6）和公式（7）的最后一行，可以看出减号右侧部分是一样的，减号左侧部分差了一个 \frac{p(x)}{q(x)}，所以上述两个方差是不同。并且分布 q(x) 与分布 p(x) 差异越大（即比值 \frac{p(x)}{q(x)} 过大或过小），方差差异也越大。

Important Sampling 的目标是求解 E_{x \backsim p(x)} [f(x)]，当该值无法直接求解时，通过求解 E_{x \backsim q(x)} \Big[ f(x)\frac{p(x)}{q(x)} \Big] 来代替。当采样的样本足够多时，这两个期望在理论上是完全相同的；但在实际操作时肯定无法完全满足采样样本足够多。那么方差越大，估计出来的值就越有可能是不准确的。所以，在实际操作时，还是会尽量选取与分布 p(x) 比较接近的分布 q(x)。

2、PPO#

之前在介绍 Policy Gradient 时，最后得到的梯度公式为如下形式：

\begin{equation}\begin{split} &\nabla \bar{R}_{\theta} = E_{(s_t, a_t) \in \pi_{\theta}} \Big[ A^{\theta}(a_t, s_t) \cdot \nabla \text{log} p_{\theta}(a_t|s_t) \Big] \\ &A^{\theta}(a_t, s_t) = \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime} - b \end{split}\end{equation}

将 Important Sampling 应用到该梯度公式中，新的梯度使用符号 \nabla J^{\theta^\prime}(\theta) 表示，这个符号里面的 \theta^\prime 和 \theta 的作用分别为：使用策略 \pi_{\theta^\prime} 与环境交互采样数据，使用采样到的这些数据对策略 \pi_{\theta} 进行更新。新的梯度计算公式以及化简过程如下所示：

\begin{equation}\begin{split} \nabla J^{\theta^\prime}(\theta) &= E_{(s_t, a_t) \in \pi_{\theta}} \Big[ A^{\theta}(a_t, s_t) \cdot \nabla \text{log} p_{\theta}(a_t|s_t) \Big] \\ &= E_{(s_t, a_t) \in \pi_{\theta^\prime}} \Big[ \frac{p_{\theta}(a_t,s_t)}{p_{\theta^\prime}(a_t,s_t)} \cdot A^{\theta^\prime}(a_t, s_t) \cdot \nabla \text{log} p_{\theta}(a_t|s_t) \Big] \\ &= E_{(s_t, a_t) \in \pi_{\theta^\prime}} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} \cdot \frac{p_{\theta}(s_t)}{p_{\theta^\prime}(s_t)} \cdot A^{\theta^\prime}(a_t, s_t) \cdot \nabla \text{log} p_{\theta}(a_t|s_t) \Big] \\ &\approx E_{(s_t, a_t) \in \pi_{\theta^\prime}} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} \cdot A^{\theta^\prime}(a_t, s_t) \cdot \nabla \text{log} p_{\theta}(a_t|s_t) \Big] \\ \end{split}\end{equation}

上述推导过程中别的地方都比较容易，只有最后一步取近似这个地方，是直接把 \frac{p_{\theta}(s_t)}{p_{\theta^\prime}(s_t)} 这一项当作 1 消去了。至于这里为什么要把这一项消去给出下面这么三项原因：

  • 这一项在实际操作时根本没有办法计算出来。【主要原因】
  • 在实际操作时一般选取与 p_{\theta}(\cdot) 比较接近的 p_{\theta^\prime}(\cdot)，所以 \frac{p_{\theta}(s_t)}{p_{\theta^\prime}(s_t)} 的值可能是趋近于 1 的。
  • 根据大量实验结果来看，消去这一项之后，训练出来的模型效果还是不错的。

至此，就得到了使用了 Important Sampling 之后的梯度公式，如下：

\begin{equation}\begin{split} &\nabla J^{\theta^\prime}(\theta) = E_{(s_t, a_t) \in \pi_{\theta^\prime}} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} \cdot A^{\theta^\prime}(a_t, s_t) \cdot \nabla \text{log} p_{\theta}(a_t|s_t) \Big] \\ &A^{\theta}(a_t, s_t) = \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime} - b \end{split}\end{equation}

同时，对应的目标函数的公式如下所示：

\begin{equation}\begin{split} &J^{\theta^\prime}(\theta) = E_{(s_t, a_t) \in \pi_{\theta^\prime}} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} \cdot A^{\theta^\prime}(a_t, s_t) \Big] \\ &A^{\theta}(a_t, s_t) = \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime} - b \end{split}\end{equation}

由 J^{\theta^\prime}(\theta) 求解梯度 \nabla J^{\theta^\prime}(\theta) 时会用到公式 \nabla f(x)=f(x) \nabla \text{log}f(x)。注意由 J^{\theta^\prime}(\theta) 求解梯度是对参数 \theta 求梯度，在其公式中的 p_{\theta^\prime}(a_t|s_t) 和 A^{\theta^\prime}(a_t, s_t) 都是与 \theta 无关的，只有 p_{\theta}(a_t|s_t) 是与 \theta 有关的。

在上面的 1.2 小节已经分析过 Important Sampling 在实际使用时最好是要求 p_{\theta}(\cdot) 与 p_{\theta^\prime}(\cdot) 比较接近，这就需要在上述目标函数的基础上再增加上一些约束，之后就得到了 PPO 算法最终的目标函数了。

2.1 PPO 目标函数#

要保证两个分布 p_{\theta}(\cdot) 与 p_{\theta^\prime}(\cdot) 比较接近，最直观的想法就是使用 KL 散度，在原来目标函数的基础上加上 KL 散度的约束，使得两个分布不要差别太大，新的目标函数公式如下所示：

\begin{equation}\begin{split} &J^{\theta^\prime}_{PPO}(\theta) = J^{\theta^\prime}(\theta) - \beta \text{KL}(\theta, \theta^\prime) \\ &J^{\theta^\prime}(\theta) = E_{(s_t, a_t) \in \pi_{\theta^\prime}} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} \cdot A^{\theta^\prime}(a_t, s_t) \Big] \\ &A^{\theta^\prime}(a_t, s_t) = \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime} - b \end{split}\end{equation}

这个操作很容易理解，在原来的目标函数 J^{\theta^\prime}(\theta) 的基础上添加一个 KL 散度的约束。

这里主要解释一下在目标函数中 KL 散度与 L1/L2 正则所起的作用的不同。如果在目标函数中添加了 L1/L2 正则，那么它主要的作用是约束模型的参数，比如 L1 正则可以让模型的参数中出现更多的0；L2 正则可以让模型的参数的方差更小。而目标函数中的 KL 散度，并不是作用于模型的参数，而是作用于模型输出的分布，它主要是保证两个模型的输出分布是相似，这两个模型的参数可以差异很大都没有问题，只要输出结果的分布是接近的就可以。

目标函数中 KL 散度前面的系数 \beta 是一个超参数，介绍一个简单的方法自动化的调整该超参数。首先对于 KL 散度设置一个最大值 KL_{max} 和一个最小值 KL_{min}，在训练过程中，如果计算出来的 KL 散度的值大于了设置的这个最大值，那么就增大 \beta；如果就算出来的 KL 散度的值小于了设置的这个最小值，那么就减小 \beta。可以写成如下形式：

\begin{equation}\begin{split} &\text{If } \quad KL(\theta, \theta^\prime) > KL_{max}, \quad \text{increase} \quad \beta \\ &\text{If } \quad KL(\theta, \theta^\prime) < KL_{min}, \quad \text{decrease} \quad \beta \end{split}\end{equation}

2.2 PPO2 目标函数#

该方法也可以称为 PPO 的截断版本，该方法的目标函数如下所示：

\begin{equation}\begin{split} &J^{\theta^\prime}_{PPO2}(\theta) = \sum_{(s_t, a_t)} \min \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} \cdot A^{\theta^\prime}(a_t, s_t), \text{clip}\Big( \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)}, 1-\epsilon, 1+\epsilon \Big) \cdot A^{\theta^\prime}(a_t, s_t) \Big] \\ &A^{\theta^\prime}(a_t, s_t) = \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime} - b \end{split}\end{equation}

该目标函数只是看起来比较长，实际上理解起来很容易，也比较直观，直接使用函数图像即可理解。

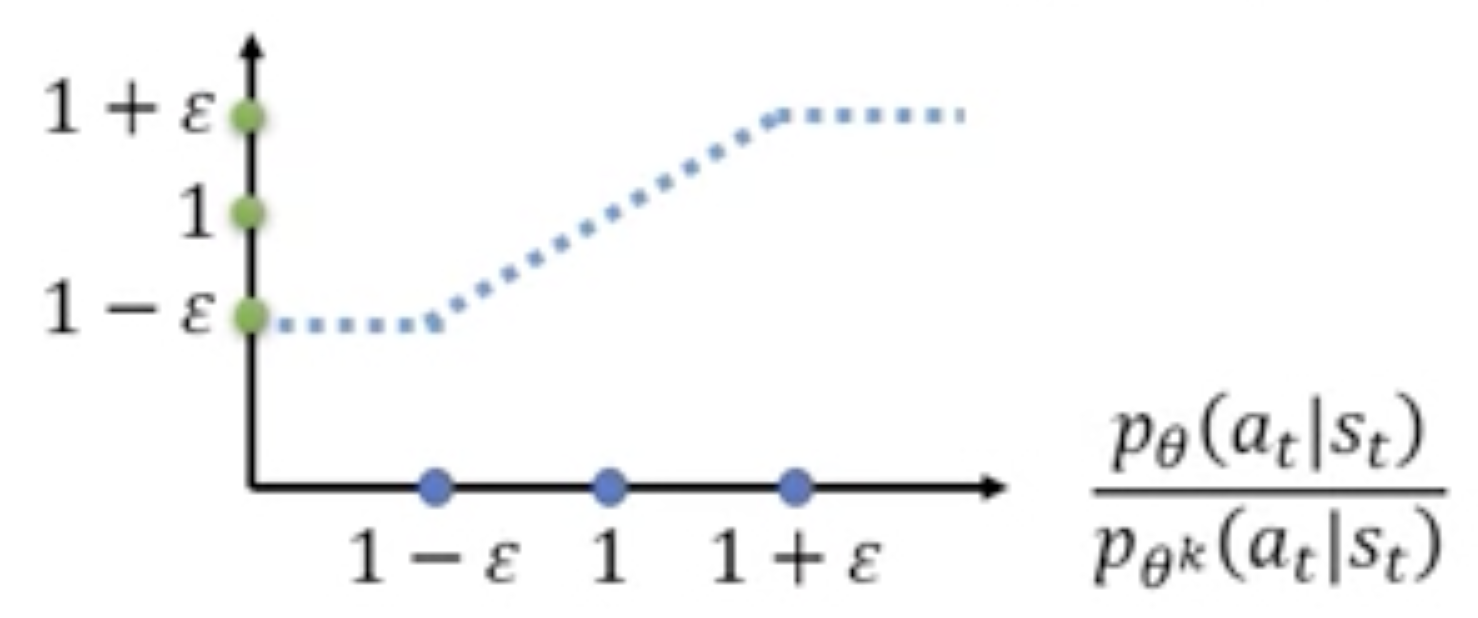
首先来看公式 \text{clip}\Big( \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)}, 1-\epsilon, 1+\epsilon \Big)，其函数图像如下所示。在下图中横坐标为 \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)}，该公式的含义为：当 \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} 的值小于 1-\epsilon 时，则截断为 1-\epsilon；当 \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} 的值大于 1+\epsilon 时，则截断为 1+\epsilon。在下述图像中可以看到，当自变量的值在 1-\epsilon 与 1+\epsilon 之间时，纵轴的值就等于横轴的值；当自变量过小或过大时就做截断。

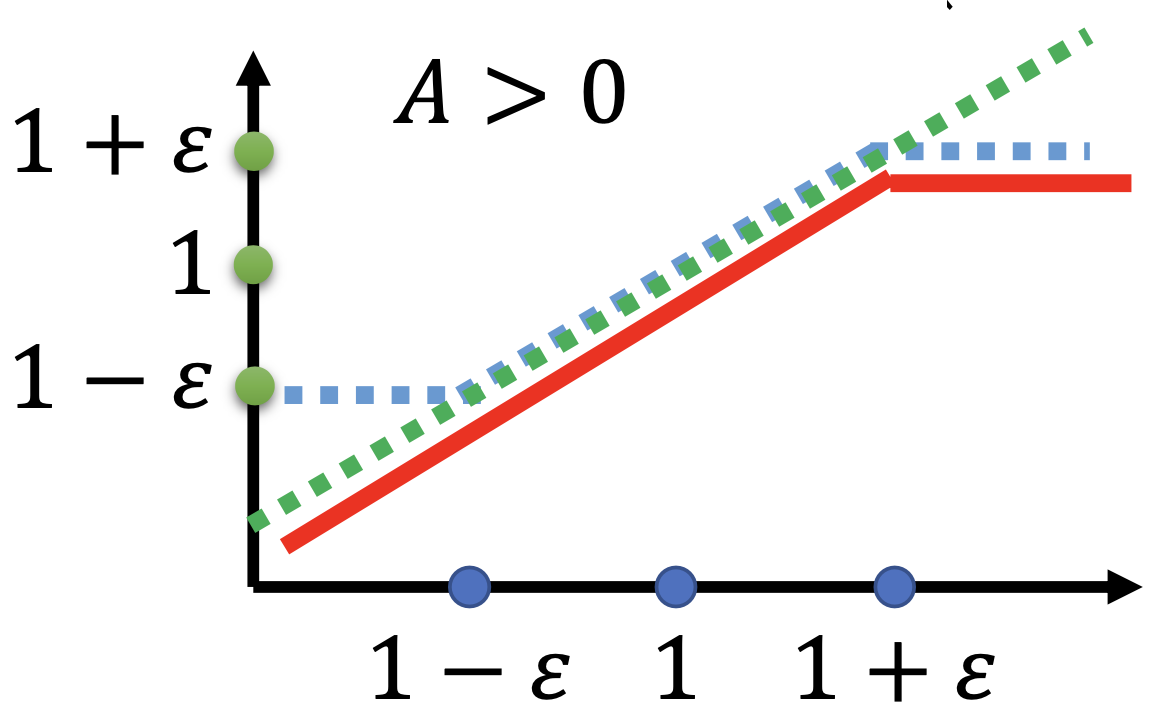
然后再来看 J^{\theta^\prime}_{PPO2}(\theta) 的函数图像。它的函数图像与 A^{\theta^\prime}(a_t, s_t) 的取值为正还是为负是有关系的，下面的左图是 A^{\theta^\prime}(a_t, s_t) 小于0时的函数图像，下面的右图是 A^{\theta^\prime}(a_t, s_t) 大于0时的函数图像。

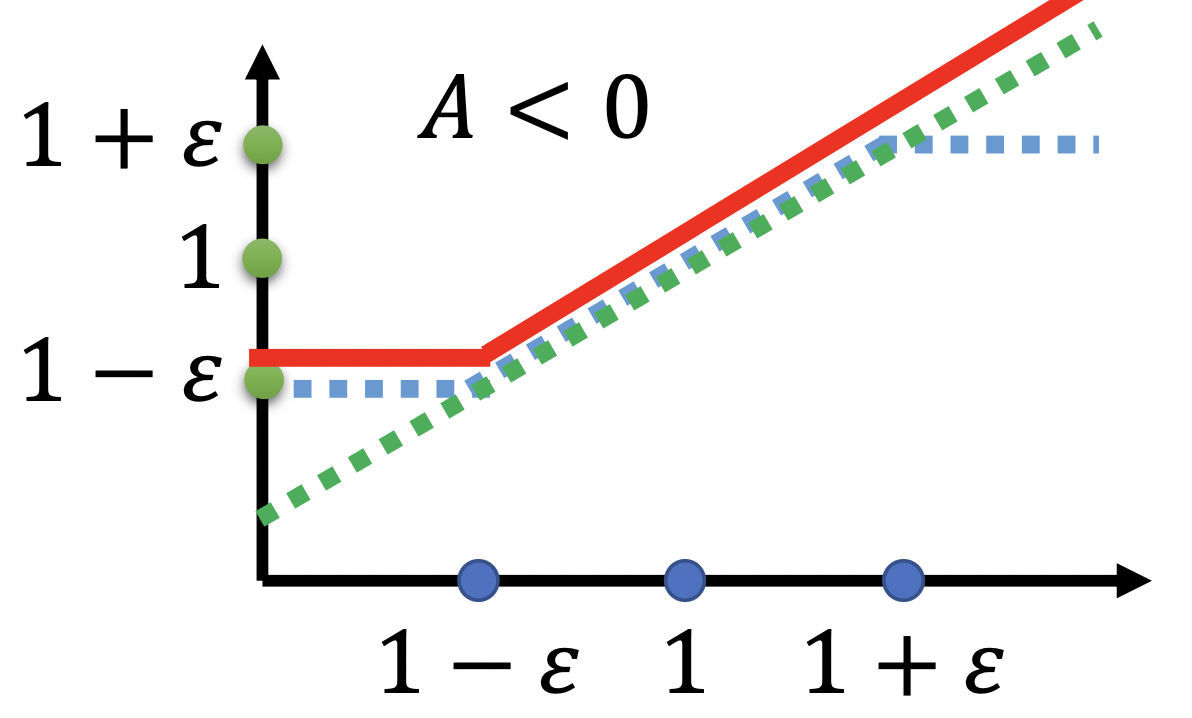对于上述左右两个图像从强化学习这个任务上也有直观的理解。当 A^{\theta^\prime}(a_t, s_t) 的取值为正时，说明当前的策略是比较好的，训练时优化的方向是增大这个策略的概率，为了不使一步优化中的步长太大，需要给他的步长设置一个上限。当 A^{\theta^\prime}(a_t, s_t) 的取值为负时，说明当前的策略是比较差的，训练时的优化方向是减小这个策略的概率，同样为了不使一步优化中的步长太大，就需要给他的步长设置一个下限。

2.3 TRPO#

Trust Region Policy Optimization（TRPO）是在 PPO 之前出现的，PPO 是在其基础上做的优化。

TRPO 这个算法无论是推导过程还是 motivation 都是比较复杂的，这里不对其做具体的介绍，只写一下它的目标函数，并且将其与PPO的目标函数做一下对比。

TRPO 的目标函数如下所示：

\begin{equation}\begin{split} &J_{TRPO}^{\theta^\prime}(\theta) = E_{(s_t, a_t) \in \pi_{\theta^\prime}} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^\prime}(a_t|s_t)} \cdot A^{\theta^\prime}(a_t, s_t) \Big] \\ &A^{\theta}(a_t, s_t) = \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime} - b \\ &s.t. \qquad \text{KL}(\theta, \theta^\prime) < \delta \end{split}\end{equation}

和 PPO 的目标函数公式（12）对比可以看出，两者非常相似。公式（12）中是把 KL 散度这个约束条件放到了目标函数中，通过对神经网络做梯度上升/梯度下降来进行优化。而 TRPO 则是把 KL 散度这个约束单独放在这里，将其作为一个有约束的问题进行优化，而有约束的优化问题向来是非常复杂的。

另外，在效果上，大量的实验表明 PPO 算法的效果等同于或者略优于 TRPO 算法。所以，相比较而言，PPO 操作相对简单，效果也相对较好，所以目前 PPO 要比 TRPO 使用的更广泛一些。

2.4 PPO 算法过程#

上面已经介绍了 PPO 和 PPO2 的目标函数，接下来介绍一下具体的算法过程。PPO 的算法如下：

  • 初始化策略参数为 \theta^0

  • LOOP：

    • 使用参数为 \theta^k 的模型与环境互动采样 (s_t, a_t, r_t, s_{t+1})，并且根据下述公式计算出 A^{\theta^k}(s_t, a_t)：
    \begin{equation}A^{\theta^k}(a_t, s_t) = \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime} - b\end{equation}
    • 使用上述采样的数据按照下述目标函数优化参数 \theta，并且上述数据可以使用多次对 \theta 进行优化：
\begin{equation}\begin{split} &J^{\theta^k}_{PPO}(\theta) = J^{\theta^k}(\theta) - \beta \text{KL}(\theta, \theta^k) \\ &\begin{split}J^{\theta^k}(\theta) &= E_{(s_t, a_t) \in \pi_{\theta^k}} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^k}(a_t|s_t)} \cdot A^{\theta^k}(a_t, s_t) \Big] \\ &\approx \sum_{(s_t, a_t)} \Big[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta^k}(a_t|s_t)} \cdot A^{\theta^k}(a_t, s_t) \Big] \end{split} \end{split}\end{equation}

将上述算法过程中的 J^{\theta^k}_{PPO}(\theta) 换为公式（14）的 J^{\theta^k}_{PPO2}(\theta) 就是 PPO2 的算法过程。

Reference#