Policy Gradient#
1、基于策略的方法#
1.1 策略 \pi#
策略 \pi 是一个参数为 \theta 的神经网络,输入是 s,输出是 a。这里的 s 是 state,一般是向量或者矩阵;这里的 a 是 action,有可能是连续的,也有可能是离散的。如果 a 是连续的那么这就是一个 regression 任务,如果 a 是离散的那么这就是一个 classification 任务。
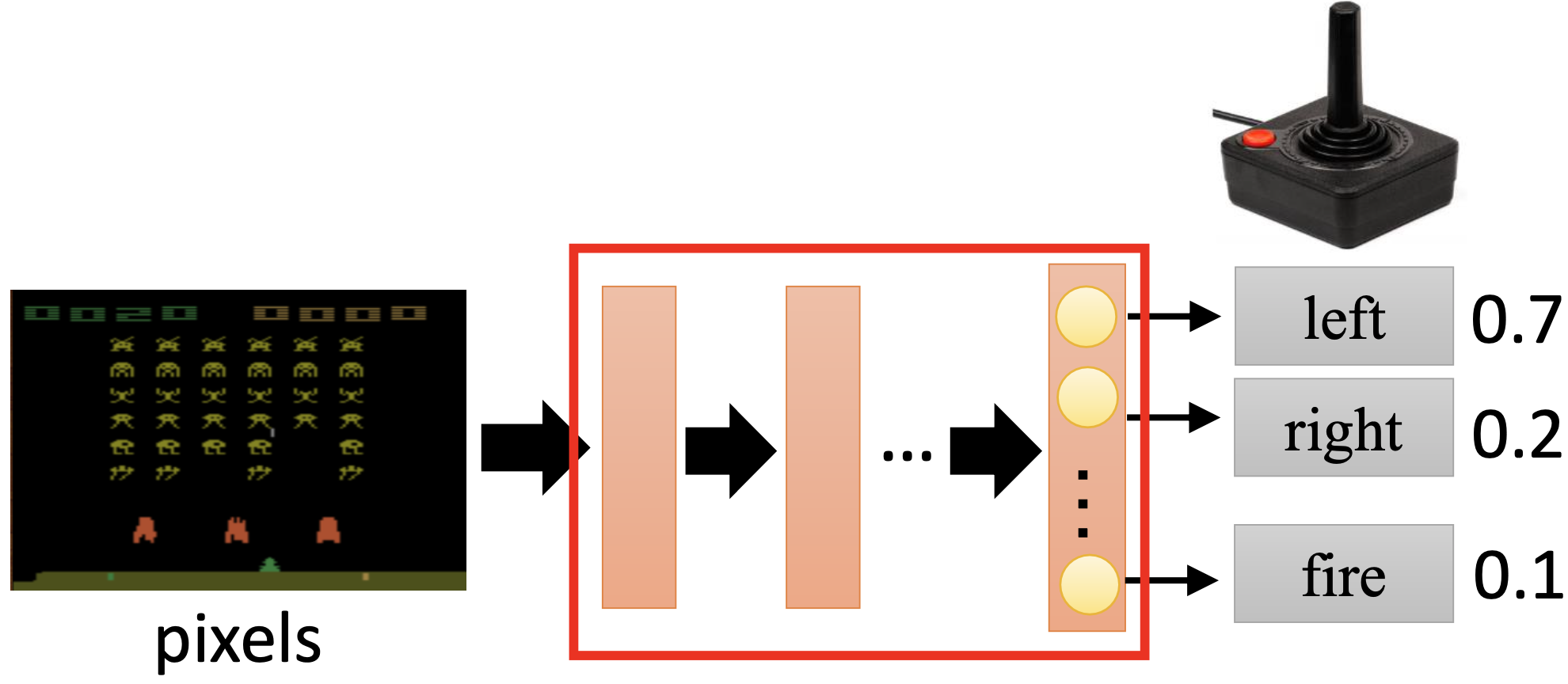
如下图所示,以一个玩游戏的任务为例。最左侧是当前游戏的一个画面,即 s,将他输入到神经网络中,输出就是三个可以执行的动作的概率,也就是 a。中间那部分神经网络就是策略 \pi。
1.2 Trajectory#
从开始时刻,到终止状态,称为一个 episode。在一个 episode 中得到的所有的 state 和 action 的序列称为 trajectory,使用符号 \tau 来表示,其公式如下:
当前策略是一个参数为 \theta 的神经网络,那么从该马尔科夫决策系统中采样出 \tau 的概率为下述公式:
1.3 奖励#
r_t 表示的是在 t 时刻的 pair 对 (s_t, a_t) 所获得的奖励。对于 trajectory 中所有 (s, a) 的 pair 对的奖励之和用 R(\tau) 表示,公式为:
(在《动手强化学习》中,这个称为回报 G)
这里的 R(\tau) 指的是一次采样得到的序列 \tau 的奖励,如果将采样过程一直进行下去,再将每个采样的奖励和加权求和,就得到了奖励和的期望,使用符号 \bar{R_{\theta}},公式为:
到这里就可以来梳理一下了,在上面所描述的强化学习中,外部环境是无法改变的,我们要做的是训练一个尽量好的策略 \pi 出来,使其能够在给定的环境中获取到尽量高的分数。也就是说我们要更新参数 \theta 使得得分 \bar{R_{\theta}} 越高越好。
所以最终要优化的目标函数就是 \bar{R}_{\theta} = \sum_{\tau}p_{\theta}(\tau) R(\tau),希望其越大越好,那么直接使用梯度上升方法就可以了。这里的参数 \theta 对应的是策略 \pi,我们更新参数 \theta 其实就是在学习和更新策略 \pi,所以该方法也称为基于策略的方法,与另外的基于值函数的方法是区分开的。
接下来按照常规做法就是求出梯度 \nabla \bar{R}_{\theta},然后做梯度上升就可以了。但是这里存在的问题是,这个梯度很难计算,所以后续就出现了多种针对这个梯度的计算方法(当然其中有一些算法是近似计算),这些针对梯度的不同的计算方法也就对应着各种基于策略的方法的变体。
2、Policy Gradient#
2.1 梯度求解#
现在已经知道了目标函数为:\bar{R}_{\theta} = \sum_{\tau} p_{\theta}(\tau) R(\tau),接下来就是求解梯度 \nabla \bar{R}_{\theta} 了,推导过程如下,这个推导过程比较繁琐,这里给每一行都添加一个行号,方便后面做说明。
从第6行到第7行是纯数学推导,这里利用了结论 \nabla f(x) = f(x) \cdot \nabla \text{log} f(x),至于该结论的证明可以查阅其他资料,这里暂时将其作为已知结论来使用。
从第7行到第8行是完全等价的,只是符号上的区别,遍历所有可能的 \tau,对其进行加权求和 \sum_{\tau} p_{\theta}(\tau) 得到的最终结果就是期望 E_{\tau \backsim p_{\theta}(\tau)}
从第7/8行到第9行是一个近似变换。第7/8行中是每个 \tau 使用自己的概率 p_{\theta}(\tau),由于该概率不好计算,那么就近似将每个 \tau 置为同等概率就是第9行公式:\frac{1}{N} \sum_{n=1}^N
从第9行到第10行并不是严格的数学变换,需要结合该问题分析。在前面已经知道 p_{\theta}(\tau) 的公式为 p_{\theta}(\tau) = p(s_1) \sum_{t=1}^T p_{\theta}(a_t|s_t)p(s_{t+1}|a_t,s_t)。其中初始状态 p(s_1) 与策略 \pi 是无关的,不随着策略的改变而改变;其中的 p(s_{t+1}|a_t,s_t) 部分是由环境决定的,也是与策略 \pi 无关的。所以在对策略 \pi 使用梯度上升方法,求解其梯度时,可以省略掉公式中的这部分。这就是第9行到第10行的变换过程。
另外,对于最终推导出来的第10行的结果,也可以很直观的理解。其中 p_{\theta}(a_t^n|s_t^n) 表示的是将 s_t^n 输入给策略 \pi 之后采取 a_t^n 的概率,其得到的pair对 (s_t^n, a_t^n) 是属于 \tau^n 中的一部分。这个 \tau^n 对应的最终得分 R(\tau^n) 越高,那么就给予其每个pair对越高的权重。最终对应到梯度上升也就是朝着 p_{\theta}(a_t^n|s_t^n) 的方向优化。当然如果 R(\tau^n) 是一个负分,那么其每个pair对对应的 p_{\theta}(a_t^n|s_t^n) 自然是朝着尽量降低采用这个 action 的方向优化。
2.2 算法过程说明#
下述公式就是最终在 policy gradient 中实际使用的求解梯度的公式:
求解出梯度之后,再使用如下公式做梯度上升就可以了:
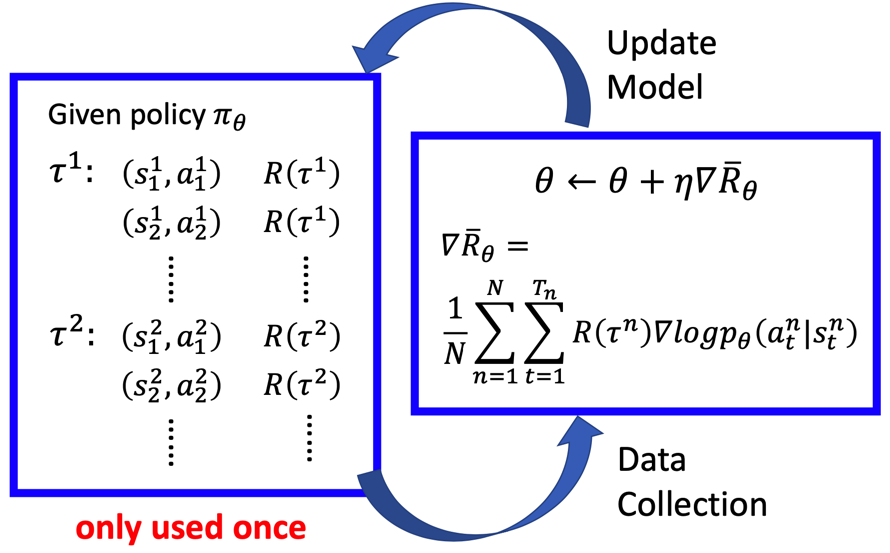
但是强化学习和有监督学习的具体训练过程有着不少的区别,下面详细说一下强化学习是如何训练的。下图中左侧蓝色框内展示的就是强化学习中数据集是什么样的。这里在理解时最好是将 \tau^1 或者 \tau^2 当作是一条样本看待,而不是将 (s_1^1, a_1^1) 当作一条样本看待。
整体来说,Policy Gradient 就是先使用策略 \pi 采样出一批样本 \{\tau^1, \tau^2, ..., \tau^N\},然后使用这批采样出的样本根据公式(11)计算出梯度,将梯度更新到策略 \pi 的参数 \theta 上。然后再使用更新后的策略 \pi 采样一批样本,再求梯度更新模型参数,一直重复该过程,直到模型效果达到预期。
前文已经说过策略 \pi 就是神经网络,如下图所示。那么每个 (s_t, a_t) 的pair对都是该网络的一个输入输出对,如下图所示,神经网络输入一个 s,输出各个 action 的概率。所以公式(11)中的 \nabla \text{log} p_{\theta} (a_t^n|s_t^n) 部分的求解就是一个常规的神经网络求梯度的问题,这个如何求解不再赘述。
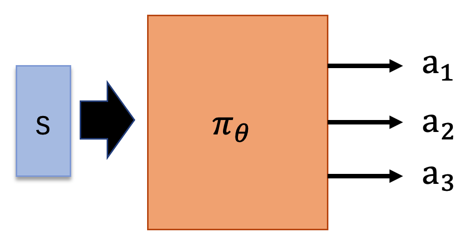
如果是有监督学习,除了模型输出一个 action,还会有一个人工标注的 action,计算模型输出结果和标签结果之间的 CE 损失然后就可以对参数 \theta 做更新了。 在强化学习这里没有人工标注的 action,这里的梯度是使用公式(11)计算出来的。
公式中的 \nabla \text{log} p_{\theta} (a_t^n|s_t^n) 部分已经会计算了,其中的 R(\tau^n) 需要注意一下,它是完成一个 episode 之后所有 r_t 的奖励之和,这里之所以使用所有奖励和的原因是:当前采取了一个 action,虽然在当前步骤没有得到太高的 reward,但是这个 action 可能对之后产生比较重要的正向的影响,使得最后得到了一个比较高的总分。所以这里 R(\tau^n) 是玩完一局游戏之后的最终得分。但是这种想法也是有着自己的问题的,一局游戏中并不是每一步的 action 都是正确的,但是在这种计算方式下一局游戏中每一个 action 都是被同等的奖励或惩罚的,后续会有算法对这里进行优化。
从上述算法过程可以看出,这里采样出 N 条样本之后,只能用于求解一次梯度,然后用该梯度更新参数 \theta 一次,之后就需要再重新采样数据。这个效率是非常低的,之后也会有方法针对该问题进行优化。
3、改进方法#
3.1 再看梯度#
由第 2.1 小节对梯度的求导可知,梯度可以用下述公式表示:
也可以用下述公式表示
其中,公式(13)是公式(14)的一个近似,其假设每个 \tau 的概率 p_{\theta}(\tau) 是相同的。后续的分析可能使用公式(13),也可能使用公式(14),哪个方便就使用哪个,不再做细致的区分。
以公式(14)为例,该梯度公式中主要有两部分需要计算,一部分是 R(\tau),另一部分是 \nabla \text{log} p_{\theta}(a_t|s_t)。其中 \nabla \text{log} p_{\theta}(a_t|s_t) 部分在第 2.2 小节已经说明过了,就是一个神经网络求解梯度的过程,比较简单。下面主要分析一下如何计算 R(\tau)。
R(\tau) 的定义为 R(\tau)=\sum_{t=1}^T r_t,直接求解该值然后代入到梯度公式中用于梯度上升会有很多问题,下面列举几个:
-
求解成本太高,像 Policy Gradient 方法中,需要先采样 N 个 \tau 之后才能够对梯度做一次更新。
-
在很多场景下 R(\tau) 可能都是非负的,比如绝大部分游戏得分都是从0开始逐渐累加,不会出现负分数。而优化时一般希望其有正有负,均值为0是最好的。
-
R(\tau) 的方差很大。首先 r_t 就是一个随机变量,每个 R(\tau) 又是 T 个 r_t 的和,累加起来之后 R(\tau) 的方差就会很大,方差大训练起来自然就会很困难。
这里只是列举了其中几个问题,实际使用时还会遇到其他的问题。对于所有基于策略的方法,可以看出,Policy Gradient 是直接使用公式(14)计算梯度,然后通过梯度上升做优化。后续的基于策略的方法都是在公式(14)的基础上,对 R(\tau) 这部分做优化,以解决或缓解其存在的问题。下一小节会介绍几个比较简单的优化方法。
3.2 改进方法#
Tip1:添加一个 Baseline
该改进主要是针对 R(\tau) 大部分情况下都是正数的问题,公式如下:
这里的 b 一般取 R(\tau) 的均值,这样 (R(\tau) - b) 这部分就是均值为0了,优化起来更容易一些。
注意:从理论上来说,不减去 b 只要采样次数足够多,那么最终得到的值就是正确的期望,但是实际操作时很难保证采样足够多的数据。
Tip2:每个pair对仅使用当前时刻之后的奖励
该改进主要是考虑在 t 时刻采取的 action 不会对之前的时刻产生影响,只会对之后的时刻产生影响。改进后的公式如下:
Tip3:对未来时刻的奖励做一个衰减
该改进主要是考虑到,虽然当前时刻采取的 action 会对之后的时刻产生影响,但是肯定是越近的时刻影响越大,越远的时刻影响越小。如果距离非常远的话,影响基本可以忽略不计了。改进后的公式如下:
其中 0<\gamma<1。
从上面的三个小优化可以看出,公式(13)中的 R(\tau) 被不断的改进,比如改进为 \Big( R(\tau^n) - b \Big)、\Big( \sum_{t^\prime=t}^T r_{t^\prime}^n - b \Big)、\Big( \sum_{t^\prime=t}^T \gamma^{t^\prime - t} r_{t^\prime}^n - b \Big)。下面对这部分再定义一个新的符号,使用 A^{\theta}(a_t, s_t) 来表示,这个被称为 Advantage Function。这样的话梯度公式就变为了:
在之后会看到对 A^{\theta}(a_t, s_t) 的更复杂的改进,比如使用一个网络来代替。这里来直观的理解一下 A^{\theta}(a_t, s_t) 所代表的含义。公式中 p_{\theta}(a_t^n|s_t^n) 表示的是输入一个状态 s_t 采取行为 a_t 的概率;A^{\theta}(a_t, s_t) 表示的是输入一个状态 s_t 采取行为 a_t 这个策略是好的,还是不好的。如果该策略是好的,那么 A^{\theta}(a_t, s_t) 就给一个正向的分数,就朝着增大这个概率的方向优化;如果是不好的,那么 A^{\theta}(a_t, s_t) 就给一个负向的分数,就朝着减小这个概率的方向优化。
4、On-policy 和 Off-policy#
On-policy 的方法指的是:"与环境互动收集数据的model" 和 "要更新的策略对应的model" 是同一个 model。
Off-policy 的方法指的是: "与环境互动收集数据的model" 和 "要更新的策略对应的model" 不是同一个 model。
上面提到的 Policy-Gradient 是 On-policy 的方法。之后介绍的 PPO 方式是 Off-policy 的方法。