[隐藏左侧目录栏][显示左侧目录栏]
旋转位置编码-RoPE
说明:本文中在符号的使用上没有区分矢量和标量。
1、问题引出
1.1 背景
整个 transformer 的前向传播过程如下所示:
\begin{equation}\begin{split}
q_m &= f_d(x_m, m) \\
k_n &= f_k(x_n, n) \\
v_n &= f_v(x_n, n) \\
a_{m,n} &= \frac{\text{exp}(\frac{q_m^{\intercal} k_n}{\sqrt{d}})}{\sum_{j=1}^N \text{exp}(\frac{q_m^{\intercal} k_j}{\sqrt{d}})} \\
o_m &= \sum_{n=1}^N a_{m,n} v_n
\end{split}\end{equation}
原始的 transformer 和 bert 这两篇论文中所使用的位置编码都是 "相加" 的方式,即如下公式:
\begin{equation}f_{\{q,k,v\}}(x_i,i)=W_{\{q,k,v\}}(x_i+p_i)\end{equation}
不过 bert 中的位置编码是可训练的,transformer 中的编码是一种绝对位置编码,公式如下所示:
\begin{equation}\begin{split}
PE_{(pos, 2i)} &= sin(pos/10000^{2i/d_{model}}) \\
PE_{(pos, 2i+1)} &= cos(pos/10000^{2i/d_{model}})
\end{split}\end{equation}
1.2 问题引出
像原始的 transformer 和 bert 这两篇论文中所使用的位置编码都是仅从构造 q、k、v 这三个向量的环节考虑,在构造旋转位置编码时加上了计算注意力权重矩阵的过程,该位置编码的原始想法基于:通过绝对位置编码的方式实现相对位置编码。这句话对应的公式为:
\begin{equation}<f(q,m),f(k,n)>=g(q,k,m-n)\end{equation}
对上述公式进行求解的过程较为复杂。下面先假设已经给出了答案,验证所给出的答案是否满足上述公式的要求。验证完成之后对旋转位置编码做一些直观的理解。待上面两部分都完成之后,再看如何由上式求解出最终的位置编码方案。
2、验证答案的正确性
2.1 基础知识
2.1.1 三角恒等式
\begin{equation}\cos(\alpha + \beta)=\cos \alpha \cos \beta - \sin \alpha \sin \beta\end{equation}
\begin{equation}\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta\end{equation}
2.1.2 复数
对形为 z=x+iy 的式子称为复数,其中 i=\sqrt{-1},x 为实部,y 为虚部,记为:
\begin{equation}x=\text{Re}(z)=\text{Re}(x+iy)\end{equation}
\begin{equation}y=\text{Im}(z)=\text{Im}(x+iy)\end{equation}
2.1.3 共轭复数
实部相同,虚部互为相反数即为共轭复数,比如复数 z=x+iy 的共轭复数为 z^*=x-iy。
2.1.4 欧拉公式
\begin{equation}e^{i\theta}=\cos \theta + i \sin \theta\end{equation}
2.1.5 Hermitian内积
设 \bold{x} 和 \bold{y} 是复向量,则其Hermitian内积为:
\begin{equation}<\bold{x},\bold{y}>=\bold{x}^{\intercal} \bold{y}^*=\sum^n_{i=1}x_i y^*_i\end{equation}
2.1.6 几个坐标系
直角坐标系和极坐标系;
实数域和复数域;
2.1.7 旋转矩阵
如下矩阵即为旋转矩阵:
\begin{equation}\begin{bmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{bmatrix}\end{equation}
向量左乘上该矩阵,对应到几何中就是:该向量的模长不变,沿逆时针方向旋转 \theta 度。
\begin{equation}\begin{bmatrix}
x^{\prime} \\
y^{\prime}
\end{bmatrix}=\begin{bmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}\end{equation}
2.2 待证明的问题
已知如下条件,要求解 f 和 g 函数:
\begin{equation}<f_q(x_m,m),f_k(x_n,n)>=g(x_m,x_n,m-n)\end{equation}
这里直接给出答案,然后验证该答案的正确性:
\begin{equation}\begin{split}
f_q(x_m, m) &= (W_q x_m) e^{im\theta} \\
f_k(x_n, n) &= (W_k x_n) e^{in\theta} \\
g(x_m, x_n, m-n) &= Re \Big[(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}\Big]
\end{split}\end{equation}
2.3 证明过程
使用欧拉公式可以将上述公式中的指数形式切换为三角函数形式,欧拉公式如下:
\begin{equation}e^{i\theta}=\cos \theta + i \sin\theta\end{equation}
上述公式中的指数形式与三角函数形式切换的公式如下:
\begin{equation}\begin{split}
e^{im\theta} &= \cos(m\theta) + i \sin(m\theta) \\
e^{in\theta} &= \cos(n\theta) + i \sin(n\theta) \\
e^{i(m-n)\theta} &= \cos((m-n)\theta) + i \sin((m-n)\theta)
\end{split}\end{equation}
仅考虑二维的情况,对 f 函数进行变换和化简。其中 q_m 如下所示:
\begin{equation}q_m = \begin{pmatrix}
q^{(1)}_m \\
q^{(2)}_m
\end{pmatrix} = W_q x_m = \begin{pmatrix}
W^{(11)}_q & W^{(12)}_q \\
W^{(21)}_q & W^{(22)}_q
\end{pmatrix}\begin{pmatrix}
x^{(1)}_m \\
x^{(2)}_m
\end{pmatrix}\end{equation}
由于是二维的,可以直接将其写为复数形式,即:q_m^{(1)} + i q_m^{(2)}。这样 f 函数就变成了纯粹的复数运算了。化简过程如下所示:
\begin{equation}f_d(x_m, m)=(W_q x_m) e^{im\theta} = q_m e^{im \theta}\end{equation}
\begin{equation}\begin{split}
q_m e^{im\theta} &= (q^{(1)}_m + i q^{(2)}_m) * (\cos(m\theta) + i \sin(m \theta)) \\
&=(q^{(1)}_m \cos(m\theta) - q^{(2)}_m \sin(m\theta)) + i(q^{(2)}_m \cos(m\theta) + q^{(1)}_m \sin(m\theta))
\end{split}\end{equation}
再将化简后的 q_m 写回向量形式,如下:
\begin{equation}\begin{split}
q_m e^{im\theta} &= \begin{bmatrix}
q^{(1)}_m \cos(m\theta) - q^{(2)}_m \sin(m\theta) \\
q^{(2)}_m \cos(m\theta) + q^{(1)}_m \sin(m\theta)
\end{bmatrix}
\end{split}\end{equation}
可以看出这就是一个旋转矩阵,公式如下所示。也就是说:对 q_m 乘上 e^{im\theta} 就等同于对 q_m 左乘上一个旋转矩阵。
\begin{equation}\begin{split}
f_d(x_m, m) &= (W_q x_m) e^{im\theta} = q_m e^{im \theta} \\
&= \begin{bmatrix}
q^{(1)}_m \cos(m\theta) - q^{(2)}_m \sin(m\theta) \\
q^{(2)}_m \cos(m\theta) + q^{(1)}_m \sin(m\theta)
\end{bmatrix} \\
&= \begin{bmatrix}
\cos(m\theta) & -\sin(m\theta) \\
\sin(m\theta) & \cos(m\theta)
\end{bmatrix}\begin{bmatrix}
q^{(1)}_m \\
q^{(2)}_m
\end{bmatrix}
\end{split}\end{equation}
上述整个对函数 f 的变形过程其实没有必要,放在这里只是为了加深理解。根据复数域极式下的乘法运算的几何含义可知:两个复数相乘,等于它们的模相乘,幅角相加。所以对向量 q_m 乘上 e^{im\theta} 的几何含义就是:模长不变,幅角向逆时针方向旋转 m\theta 度。
上面求解出了 f_q 的矩阵形式,下面使用同样的方法求解 f_k 的矩阵形式,结果如下:
\begin{equation}\begin{split}
f_k(x_n,n) &= (W_k x_n) e^{in\theta} = k_n e^{in\theta} \\
&= \begin{bmatrix}
k_n^{(1)} \cos(n\theta) - k_n^{(2)} \sin(n\theta) \\
k_n^{(2)} \cos(n\theta) + k_n^{(1)} \sin(n\theta)
\end{bmatrix} \\
&= \begin{pmatrix}
\cos(n\theta) & -\sin(n\theta) \\
\sin(n\theta) & \cos(n\theta)
\end{pmatrix}\begin{pmatrix}
k^{(1)}_n \\
k^{(2)}_n
\end{pmatrix}
\end{split}\end{equation}
至此,原始公式中等号左侧的两个就都变形完成了。下面对 g 函数做一下变形。
\begin{equation}g(x_m, x_n, m-n) = Re \Big[(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}\Big]\end{equation}
其中:
\begin{equation}\begin{split}
W_q x_m &= q_m = q^{(1)}_m + i q^{(2)}_m \\
W_k x_n &= k_n = k^{(1)}_n + i k^{(2)}_n \\
(W_k x_n)^* &= k_n^* = k^{(1)}_n - i k^{(2)}_n \\
e^{i(m-n)\theta} &= \cos((m-n)\theta) + i \sin((m-n)\theta)
\end{split}\end{equation}
代进去继续变形得到:
\begin{equation}\begin{split}
&\quad g(x_m, x_n, m-n) \\
&= Re \Big[(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}\Big] \\
&= Re \Big[ \Big(q^{(1)}_m + i q^{(2)}_m \Big) \Big(k^{(1)}_n - i k^{(2)}_n \Big) \Big(\cos((m-n)\theta) + i \sin((m-n)\theta) \Big) \Big]\\
&= Re \Big[ \Big((q^{(1)}_mk^{(1)}_n + q^{(2)}_mk^{(2)}_n) +i(q^{(2)}_mk^{(1)}_n - q^{(1)}_mk^{(2)}_n) \Big) \Big(\cos((m-n)\theta) + i \sin((m-n)\theta) \Big) \Big]\\
&= (q^{(1)}_mk^{(1)}_n + q^{(2)}_mk^{(2)}_n) \cos \big((m-n)\theta\big) - (q^{(2)}_mk^{(1)}_n - q^{(1)}_mk^{(2)}_n) \sin \big((m-n)\theta \big)
\end{split}\end{equation}
最后,就是把等号左侧的两个式子相乘得到结果,看起是否和等号右侧部分相同就可以了:
\begin{equation}\begin{split}
f_q(x_m,m) &= \begin{bmatrix}
q^{(1)}_m \cos(m\theta) - q^{(2)}_m \sin(m\theta) \\
q^{(2)}_m \cos(m\theta) + q^{(1)}_m \sin(m\theta)
\end{bmatrix} \\
f_k(x_n,n) &= \begin{bmatrix}
k_n^{(1)} \cos(n\theta) - k_n^{(2)} \sin(n\theta) \\
k_n^{(2)} \cos(n\theta) + k_n^{(1)} \sin(n\theta)
\end{bmatrix} \\
\end{split}\end{equation}
\begin{equation}\begin{split}
&\quad <f_q(x_m,m),f_k(x_n,n)> \\
&= \Big(q^{(1)}_m \cos(m\theta) - q^{(2)}_m \sin(m\theta)\Big)\Big(k_n^{(1)} \cos(n\theta) - k_n^{(2)} \sin(n\theta)\Big) \\
&\quad + \Big(q^{(2)}_m \cos(m\theta) + q^{(1)}_m \sin(m\theta)\Big)\Big(k_n^{(2)} \cos(n\theta) + k_n^{(1)} \sin(n\theta)\Big) \\
&= q^{(1)}_m \cos(m\theta) k^{(1)}_n \cos(n\theta) - q^{(1)}_m \cos(m\theta) k^{(2)}_n \sin(n\theta) \\
&\quad - q^{(2)}_m \sin(m\theta) k^{(1)}_n \cos(n\theta) + q^{(2)}_m \sin(m\theta) k^{(2)}_n \sin(n\theta) \\
&\quad + q^{(2)}_m \cos(m\theta) k^{(2)}_n \cos(n\theta) + q^{(2)}_m \cos(m\theta) k^{(1)}_n \sin(n\theta) \\
&\quad + q^{(1)}_m \sin(m\theta) k^{(2)}_n \cos(n\theta) + q^{(1)}_m \sin(m\theta) k^{(1)}_n \sin(n\theta)
\end{split}\end{equation}
使用上三角恒等式,得到:
\begin{equation}\begin{split}
&\quad <f_q(x_m,m),f_k(x_n,n)> \\
&= q^{(1)}_mk^{(1)}_n \Big(\cos(m\theta)\cos(n\theta)+\sin(m\theta)\sin(n\theta) \Big) \\
&\quad + q^{(1)}_mk^{(2)}_n \Big(-\cos(m\theta)\sin(n\theta)+\sin(m\theta)\cos(n\theta) \Big) \\
&\quad + q^{(2)}_mk^{(1)}_n \Big(-\sin(m\theta)\cos(n\theta)+\cos(m\theta)\sin(n\theta) \Big) \\
&\quad + q^{(2)}_mk^{(2)}_n \Big(\sin(m\theta)\sin(n\theta)+\cos(m\theta)\cos(n\theta) \Big) \\
&= q^{(1)}_mk^{(1)}_n\cos((m-n)\theta) + q^{(1)}_mk^{(2)}_n\sin((m-n)\theta) \\
&\quad - q^{(2)}_mk^{(1)}_n\sin((m-n)\theta) + q^{(2)}_mk^{(2)}_n\cos((m-n)\theta) \\
&=(q^{(1)}_mk^{(1)}_n+q^{(2)}_mk^{(2)}_n)\cos((m-n)\theta) + (q^{(1)}_mk^{(2)}_n-q^{(2)}_mk^{(1)}_n)\sin((m-n)\theta) \\
&=(q^{(1)}_mk^{(1)}_n+q^{(2)}_mk^{(2)}_n)\cos((m-n)\theta) - (q^{(2)}_mk^{(1)}_n-q^{(1)}_mk^{(2)}_n)\sin((m-n)\theta) \\
&= g(x_m,x_n,m-n)
\end{split}\end{equation}
到此,证明完毕。
3、直观理解该位置编码在做什么
3.1 完整公式
第2小节的整个证明过程都是在二维的情况下证明的,需要将其扩展到高维情况。高维情况时以矩阵的形式进行表示,公式如下:
\begin{equation}f_{\{q,k\}}(x_m,m)=R^d_{\Theta,m}W_{\{q,k\}}x_m\end{equation}
上面公式中的 R^d_{\Theta,m} 是一个由多个小二维旋转矩阵拼接的大矩阵。如下图所示,左侧的矩阵即为 R^d_{\Theta,m}:

其中 \theta_i 的公式为:
\begin{equation}\theta_i = 10000^{-2(i-1)/d} \qquad i=1,2,...,d/2\end{equation}
3.2 物理含义
3.2.1 直观理解
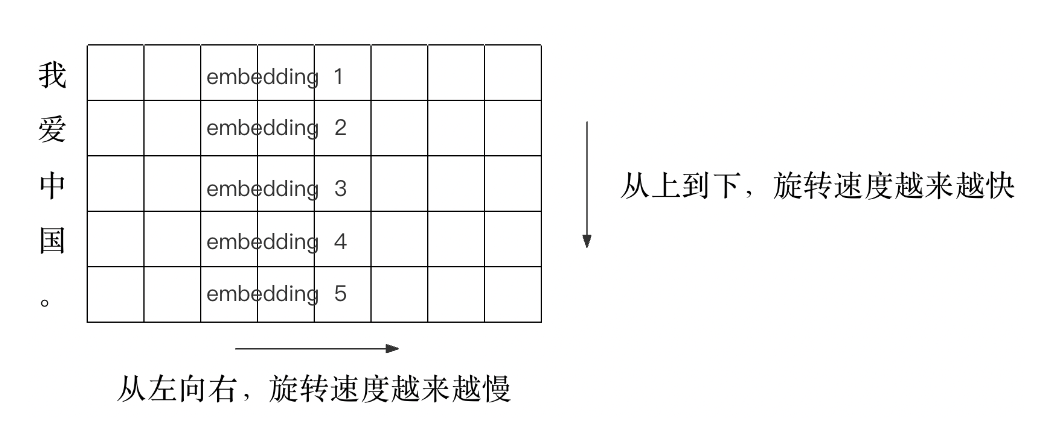
下图是旋转位置编码的一个直观理解的图片。下图中的这条样本总共六个token:Enhanced、Transformer、with、Rotary、Position、Embedding,每个 token 对应一个 d 维的向量。把向量中的分量两两分组,对每组分量做一个旋转。

3.2.2 旋转的角度大小
每个 token 的每组分量的旋转角度为 m\theta_i,其中 \theta_i 的公式为 \theta_i = 10000^{-2(i-1)/d},下面先分析其增减性。(特别注意这里有两个不同维度的变量,后续的所有优化和改进都是在这两个变量上做文章)
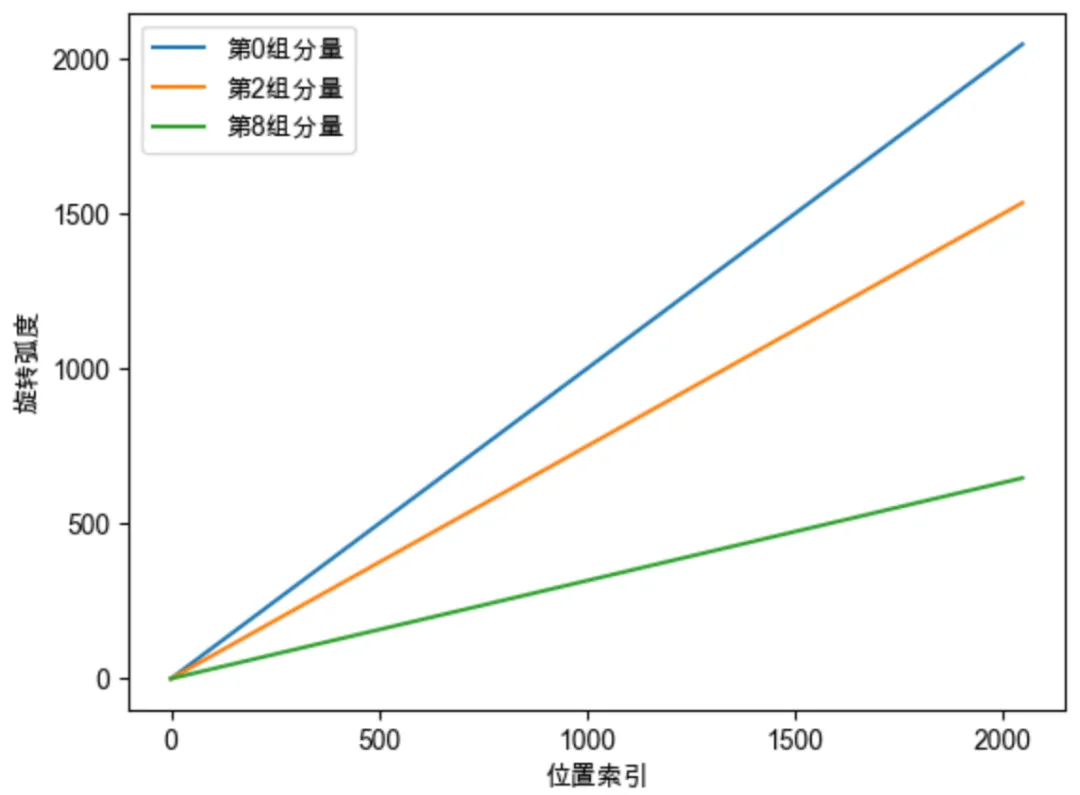
对于每个token所处的位置 m 的不同,旋转角度的差异如下图所示:
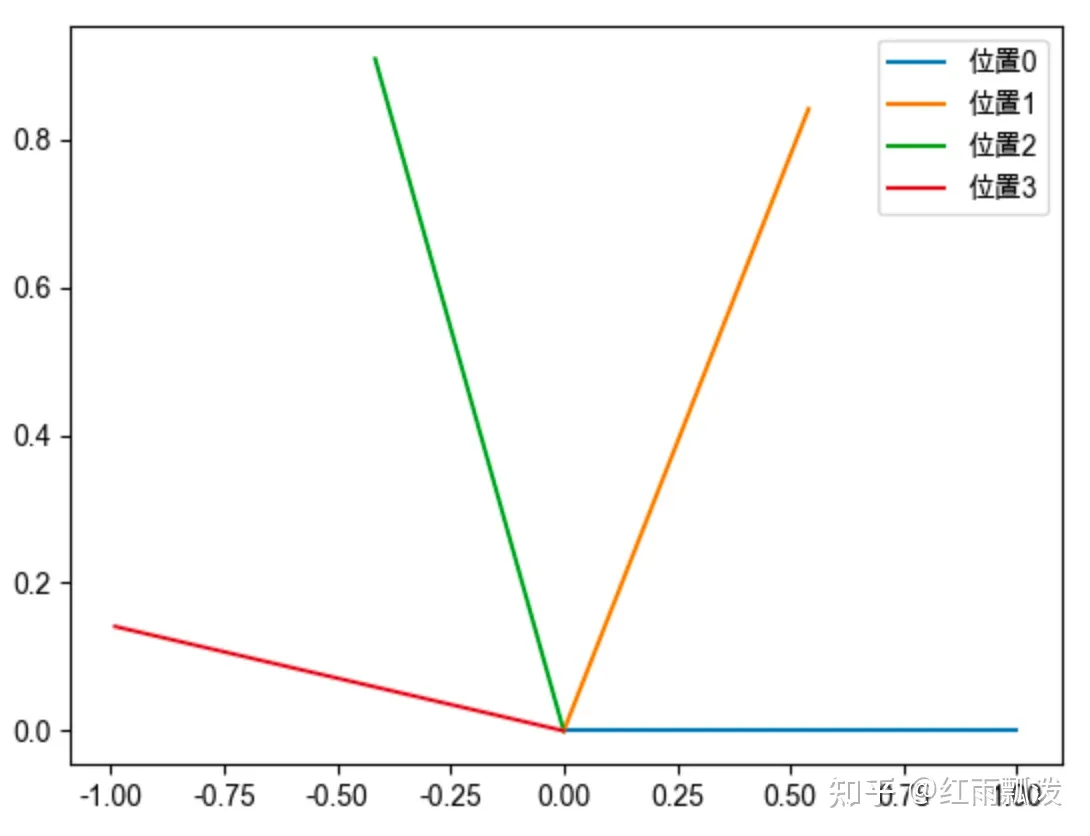
对于分量位置 i 的不同,旋转角度的差异如下图所示:
4、问题求解
直接见作者的原始文章,写的非常好:https://kexue.fm/archives/8265#%E6%B1%82%E8%A7%A3%E8%BF%87%E7%A8%8B
下面补充一些推导过程。
原文章中公式(6)中的最后一个等号
由于初始条件中 f(q,0)=q、f(k,0)=k,所以当 m=0 时,f(q,m)=R_f(q,m)e^{i\Theta_f(q,m)}=R_f(q,m),
\begin{equation}f(q,0)f(k,0)=R_f(q,0) R_f(k,0) e^{i\Theta_f(q,0)} e^{i\Theta_f(k,0)} = qk\end{equation}
由复数的极式下向量的乘法可知,qk的模就等于 q 的模乘以 k 的模。
原文章中公式(8)的推导
已知:
\begin{equation}\varphi(m)=\Theta_f(q,m)-\Theta(q) \end{equation}
\begin{equation}\varphi(m)=\Theta_f(k,m)-\Theta(k) \end{equation}
简单变换可得:
\begin{equation}\Theta_f(q,m)=\varphi(m)+\Theta(q) \end{equation}
\begin{equation}\Theta_f(k,m)=\varphi(m)+\Theta(k) \end{equation}
将上述两个式子代入到原文章中公式(5)的第二个式子可得:
\begin{equation}\Big(\varphi(m)+\Theta(q)\Big)-\Big(\varphi(m)+\Theta(k)\Big)=\Theta_g(q,k,m-n)\end{equation}
将 n=m-1 代入上式之后,做一个简单的变换就得到原文章中的公式(8)。原文章中的公式(8)的等号右侧里面 q 和 k 都是定值,只有位置 m 和分量的索引 i 是变量。所以等号后侧也是一个定值,所以 \varphi(m) 是一个等差数列。
Reference
其他
该种位置编码的整个求解公式都基于一句话:通过绝对位置编码的方式实现相对位置编码。这句话对应的公式为:
\begin{equation}<f(q,m),f(k,n)>=g(q,k,m-n)\end{equation}
这里看一下右半部分求解之后的最终结果(注意该结果仅为理论结果,代码实现中是按照上述公式的左侧部分实现的)。下图是对于整个注意力权重矩阵求解之后的结果,可以看出在最终的结果中仅有 m-n 这一项,不存在单独的 m 或者 n,这也就是说最终的注意力权重仅跟两个 token 之间的相对位置有关,与每个 token 的绝对位置是无关的。

上图出自:Extending Context Window of Large Language Models via Positional Interpolation