[隐藏左侧目录栏][显示左侧目录栏]

Q-learning、DQN、以及 DQN 的改进算法#

DQN 的全称是 Deep Q-Network，其中的 Q 就是指 Q-Learning。 从名字上就能看出，该方法指的是把 Q-Learning 和 DNN[Deep Neural Network] 结合起来。所以这两种方法没有本质区别，比如原来是一个(状态, 动作)的概率表，在 DQN 中把其换为了一个神经网络。所以本文不再单独介绍 Q-learning 方法，而是直接介绍 DQN 方法。

1、估计状态价值函数 V^{\pi}(s)#

注意：这一小节描述的是如何估计状态价值函数，这里不涉及如何设计策略 \pi。所以在这一小节中是假设已经有了一个策略 \pi 的前提下，讨论如何估计该策略 \pi 的状态价值函数。

状态价值函数的公式如下：

\begin{equation}V^\pi(s)=E_{\pi}(G_t|S_t=s)\end{equation}

1.1 MC 方法#

MC 全称为 Monte-Carlo。蒙特卡洛方法使用策略 \pi 跟环境做互动，收集每个状态 s 和其对应的回报 G 的数据对 (s, G)，使用收集到的这些数据和下图的神经网络就可以估计出状态价值函数 V^{\pi}(s)：

图1

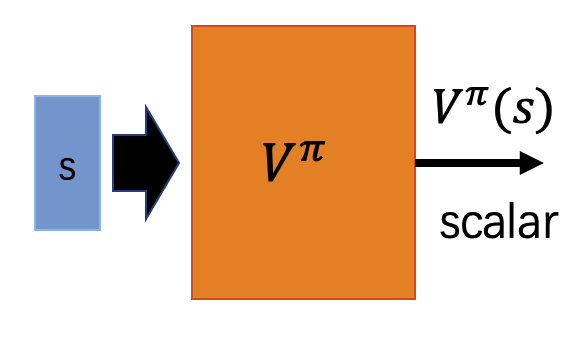上图中的神经网络 V^{\pi} 就是状态价值函数，它的输入是状态 s，输出是 V^{\pi}(s)，标签是 G，要学习的目标是让输出值 V^{\pi} 与标签 G 相同。其中 V^{\pi} 和 G 都是标量，按照 regression 任务训练即可。

该方法的缺点很明显，需要完成整个 episode 才能收集到一条样本 (s, G)，有些任务完成整个 episode 耗时是比较长的，所以该方法收集数据的成本很高。

1.2 TD 方法#

TD 全称为 Temporal-Difference。相比于蒙特卡洛方法需要完成整个 episode 之后才能收集到一条数据，时序差分方法则是策略 \pi 每一次与环境互动都可以收集到一条数据。时序差分方法会利用到时序差分公式，如下：

\begin{equation}V^{\pi}(s_t) = r_t + V^{\pi}(s_{t+1})\end{equation}

使用策略 \pi 与环境互动一步，可以得到数据：(s_t, a_t, r_t, s_{t+1})，收集多条样本数据，按照下图所示的结构进行训练：

图2

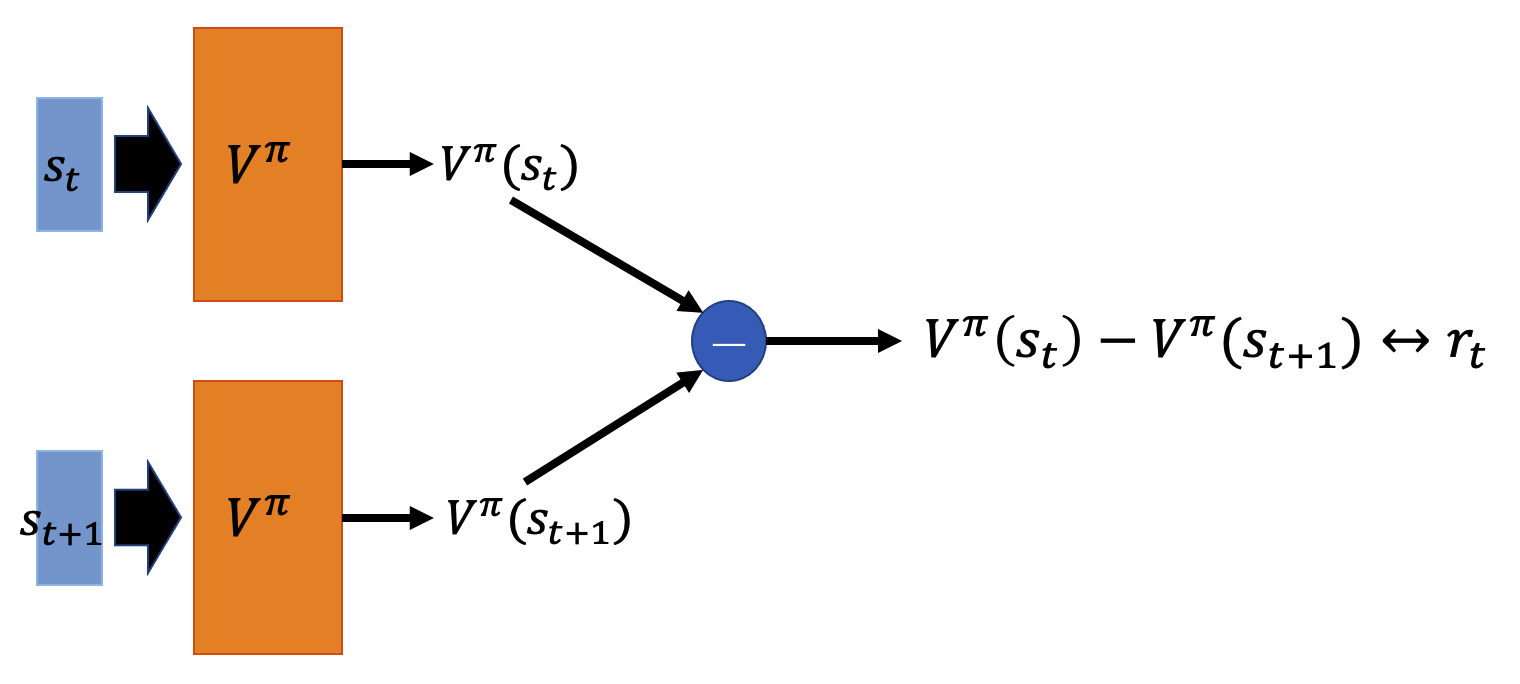上图中的神经网络 V^{\pi} 就是状态价值函数，上图中两个 V^{\pi} 是同一个模型。给该模型输入 s_t 其输出值为 V^{\pi}(s_t)，给该模型输入 s_{t+1} 其输出值为 V^{\pi}(s_{t+1})。按照时序差分公式可以知道 V^{\pi}(s_t) 与 V^{\pi}(s_{t+1}) 之间差了一个 r_t，所以上述模型的学习目标是让 V^{\pi}(s_t) - V^{\pi}(s_{t+1}) 与标签 r_t 相同。其中 V^{\pi}(s_t) - V^{\pi}(s_{t+1}) 和 r_t 都是标量，也是按照 regression 任务训练即可。

1.3 MC vs TD#

在 MC 方法中，它要学习的标签是 G，而 G 的方差是比较大的，它的公式为：

\begin{equation}G=\sum_{t=0}^\infty \gamma^t r_t\end{equation}

策略 \pi 每一次跟环境交互得到的 r_t 就已经是一个随机变量，G 又是每个 episode 中所有 r_t 之和，所以 G 的方差是要比 r_t 的方差是要大的。

在 TD 中要拟合的是 r_t，r_t 的方差是相对比较小的，这是 TD 相比于 MC 的优点。但是 TD 方法要拟合的公式为 V^\pi(s_t) - V^\pi(s_{t+1})=r_t，这个拟合公式只能保证 V^\pi(s_t) 与 V^\pi(s_{t+1}) 的差值是准确的，却无法保证 V^\pi(s_t) 和 V^\pi(s_{t+1}) 各自的值是准确的。所以该方法是有偏的，这是 TD 方法的劣势。

MC 方法无偏但是方差大，TD 方法方差小但是有偏。有一种改进的多步 TD 方法可以看作是结合了 TD 和 MC 的优点。想法其实很简单，TD 方法是仅采用和环境的一步交互得到的数据为 (s_t, a_t, r_t, s_{t+1})，其差分方程也是仅用一步估计，也就是下式：

\begin{equation}V^{\pi}(s_t) = r_t + V^{\pi}(s_{t+1})\end{equation}

多步 TD 方法是和环境交互 N 步得到的数据为 (s_t, a_t, r_t, s_{t+1}, a_{t+1}, r_{t+1}, ..., s_{t+N}, a_{t+N}, r_{t+N}, s_{t+N+1})，其差分方程也是使用 N 步估计，也就是下式：

\begin{equation}V^{\pi}(s_t) = \sum_{t^\prime=t}^{t+N} r_{t^\prime} + V^\pi(s_{t+N+1})\end{equation}

在上述公式里，如果 N=1，那么就是 TD 方法；如果 N 是一直到 episode 结束，那么就是 MC 方法。上述公式是 MC 方法与 TD 方法的 balance。

2、估计动作价值函数 Q^{\pi}(s, a)#

注意：这一小节描述的是如何估计动作价值函数，这里不涉及如何设计策略 \pi。所以在这一小节中是假设已经有了一个策略 \pi 的前提下，讨论如何估计该策略 \pi 的动作价值函数。

动作价值函数的公式如下：

\begin{equation}Q^\pi(s,a)=E_\pi(G_t|S_t=s,A_t=a)\end{equation}

2.1 MC 方法#

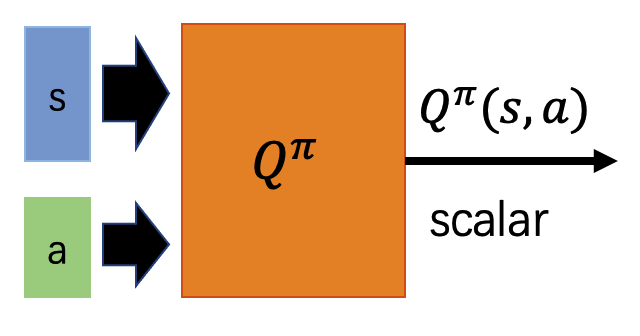
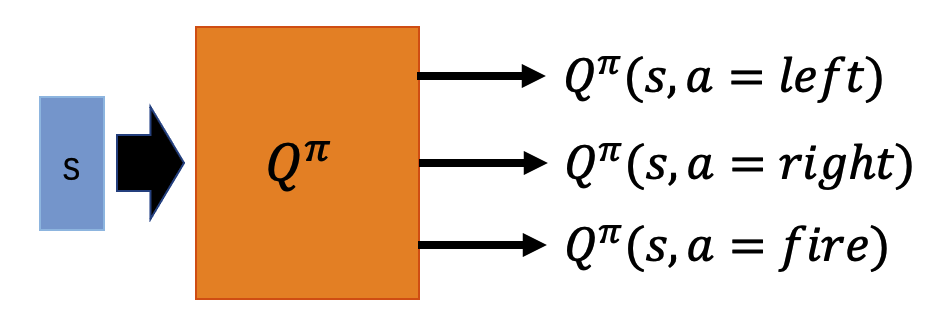
在估计动作价值函数时的模型结构一般有如下图的两种设计。左图的输入是状态 s 和动作 a，输出是 dependent 这个 s 和 a 的价值。右图输入是状态 s，输出是在动作 s 下分别采取每个动作 a 时的价值。注意右图这种设计只有在动作 a 为离散时才可以使用这种模型结构。

图3 图4

使用策略 \pi 跟环境做互动，收集在每个状态 s 下，策略采取不同的动作 a 所获取的回报 G。

如果采用上图中左图的模型结构，那么输入是状态 s 和动作 a，输出为 Q^\pi(s,a)，标签为 G，其中 Q^\pi(s,a) 和 G 都是标量，按照 regression 任务处理即可。

如果采用上图中右图的模型结构，那么输入是状态 s，输出是不同动作下的价值 Q^\pi，标签是不同动作下的回报 G，也是按照 regression 任务处理即可。

2.2 TD 方法#

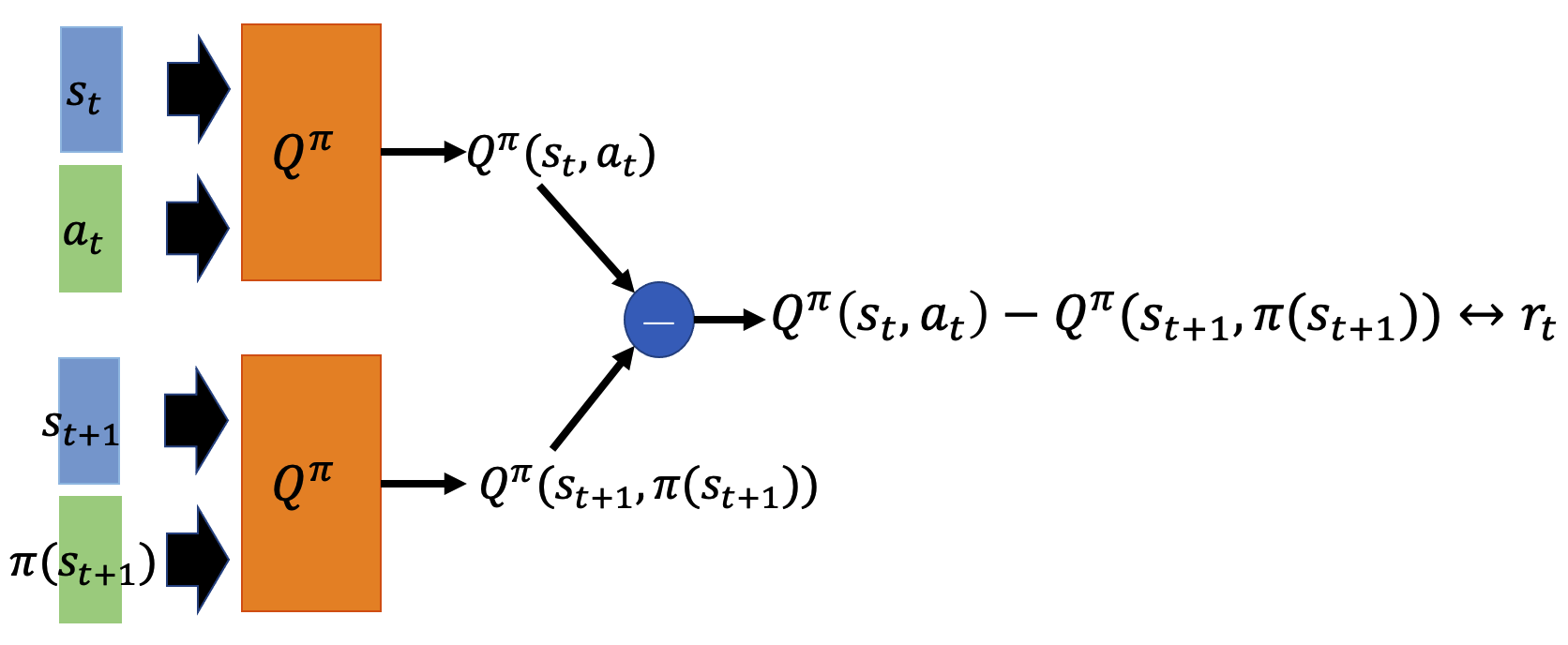
使用 TD 方法估计动作价值函数的模型结构如下图，与估计状态价值函数是非常相似的，模型结构就不再说明了。差分公式中有一项需要注意，如下公式（7）是估计动作价值函数时使用的差分公式。注意在 t+1 时刻，模型 Q^\pi 的输入不是 a_{t+1}，而是 \pi(s_{t+1})。原因是给定状态 s_{t+1} 之后策略 \pi 不一定采取动作 a_{t+1}，它可能采取任何的动作，在下述公式中加号右侧的这一项是要估计给定状态 s_{t+1} 之后，采取所有可能的动作 a 的价值的期望。这里使用符号 \pi(s_{t+1}) 就是表示这里可能是任何的动作。

\begin{equation}Q^{\pi}(s_t, a_t) = r_t + Q^{\pi}(s_{t+1}, \pi(s_{t+1}))\end{equation}
图5

3、DQN 算法#

在该小节中假设所有的 action 都是离散的，至于连续的 action 如何处理在之后的内容中讨论。

在上一小节中已经有方法能够估计出动作价值函数 Q^{\pi}(s, a)，有了动作价值函数 Q^{\pi}(s, a) 之后就可以基于其进行强化学习了。总体的思路是：先有一个不是那么好的策略 \pi，比如可以随机初始化一个策略 \pi。估计出这个策略 \pi 相应的动作价值函数 Q^{\pi}(s, a)，然后可以使用 "某个方法" 从 Q^{\pi}(s, a) 得到一个新的策略 \pi^\prime，并且该方法可以保证新得到的策略 \pi^\prime 是比之前的策略 \pi 更优的。这样使用新策略 \pi^\prime 替换原来的策略 \pi 之后再重复上述过程，每次都能够得到一个更优的策略，就能够一直迭代训练下去了。后面就介绍这里提到的 "某个方法" 具体是如何操作的。

首先给出该方法所能达到的功能：该方法可以从 Q^{\pi}(s, a) 中得到一个策略 \pi^\prime，并且能够保证这个新的策略 \pi^\prime 要比之前的策略 \pi 更优。

对于 "策略 \pi^\prime 比策略 \pi 更优" 这种说法，给出一个严格的公式定义，当策略 \pi^\prime 和策略 \pi 满足下述公式时，就说策略 \pi^\prime 是比策略 \pi 更优的。这个公式可以直观的理解为：给定状态 s 之后，策略 \pi^\prime 所选取的动作能够比策略 \pi 所选取的动作获取更高的回报 G。

\begin{equation}V^{\pi^\prime}(s) \geqslant V^{\pi}(s)\end{equation}

接下来给出该方法具体是如何操作的。

从 Q^{\pi}(s, a) 中得到策略 \pi^\prime 的公式如下所示：

\begin{equation}\pi^\prime = \text{argmax}_a Q^{\pi}(s, a)\end{equation}

首先来直观的理解该公式是在做什么，然后在 3.1 小节中证明该公式得到的结果能够满足 V^{\pi^\prime}(s) \geqslant V^{\pi}(s)。上述公式中 Q^{\pi}(s, a) 表示给定状态 s 时，如果策略 \pi 采取了动作 a 所能获得的价值。\text{argmax}_a Q^{\pi}(s, a) 则表示给定状态 s 时，将所有能够采取的动作 a 逐个求解一遍 Q^\pi(s,a) 的值，选出能够使 Q^\pi(s,a) 最大的那个动作 a。之后再遇到给定状态 s 时，就采取该动作。这就是策略 \pi^\prime。

3.1 DQN 有效性的证明#

这里主要是证明使用公式 a=\text{argmax}_a Q^\pi(s, a) 得到的 \pi^\prime 能够满足 V^{\pi^\prime}(s) \geqslant V^\pi(s)。

首先有如下公式成立：

\begin{equation}V^\pi(s)=Q^\pi(s, \pi(s)) \leqslant \text{max}_a Q^\pi(s,a) = Q^\pi(s, \pi^\prime(s))\end{equation}

基于上述公式：

\begin{equation}\begin{split} V^\pi(s) &\leqslant Q^\pi(s, \pi^\prime(s)) \\ &= E\Big[ r_t + V^\pi(s_{t+1})|s_t=s,a_t=\pi^\prime(s_t) \Big] \\ &\leqslant E\Big[r_t + Q^\pi(s_{t+1}, \pi^\prime(s_{t+1}))|s_t=s,a_t=\pi^\prime(s_t) \Big] \\ &= E\Big[r_t + t_{t+1} + V^\pi(s_{t+2})| \cdots \Big] \\ &\leqslant E\Big[r_t + t_{t+1} + Q^\pi(s_{t+2}, \pi^\prime(s_{t+2}))| \cdots \Big] \\ &\cdots \\ &\leqslant V^{\pi^\prime}(s) \end{split}\end{equation}

3.2 DQN 算法过程#

训练过程如下，在该训练的算法中估计动作价值函数使用的是 TD 算法：

  • 初始化 Q-function 的模型，记为 Q

  • 循环遍历多个 episode，对于每个 episode：

    • 遍历每个时刻 t：

      • 给定状态 s_t，使用模型 Q，依照下述策略选出动作 a_t：
      a_t = \text{argmax}_a Q(s_t, a_t)

      • 有了 s_t 和 a_t 之后，跟环境做交互可以得到 r_t 和 s_{t+1}；输入到模型 Q 中可以得到 Q(s_t, a_t)；

      • 给定状态 s_{t+1}，使用模型 Q 依照下述公式遍历所有可能的动作 a，计算出要拟合的目标：

      y = r_t + \text{max}_a Q(s_{t+1}, a)
      • 最后就是 Q(s_t, a_t) 作为 logits，y 作为 label，按照 regression 任务对模型 Q 进行优化就可以了；

推理过程比训练过程简单许多，如下：

  • 给定状态 s_t，使用训练好的模型 Q，依照下述策略选出动作 a_t：
a_t = \text{argmax}_a Q(s_t, a_t)

  • 有了 s_t 和 a_t 之后，与环境交互能够得到 s_{t+1}；

  • 重复上述两步，直到生成整个 episode；

4、DQN 的改进#

4.1 Target Network#

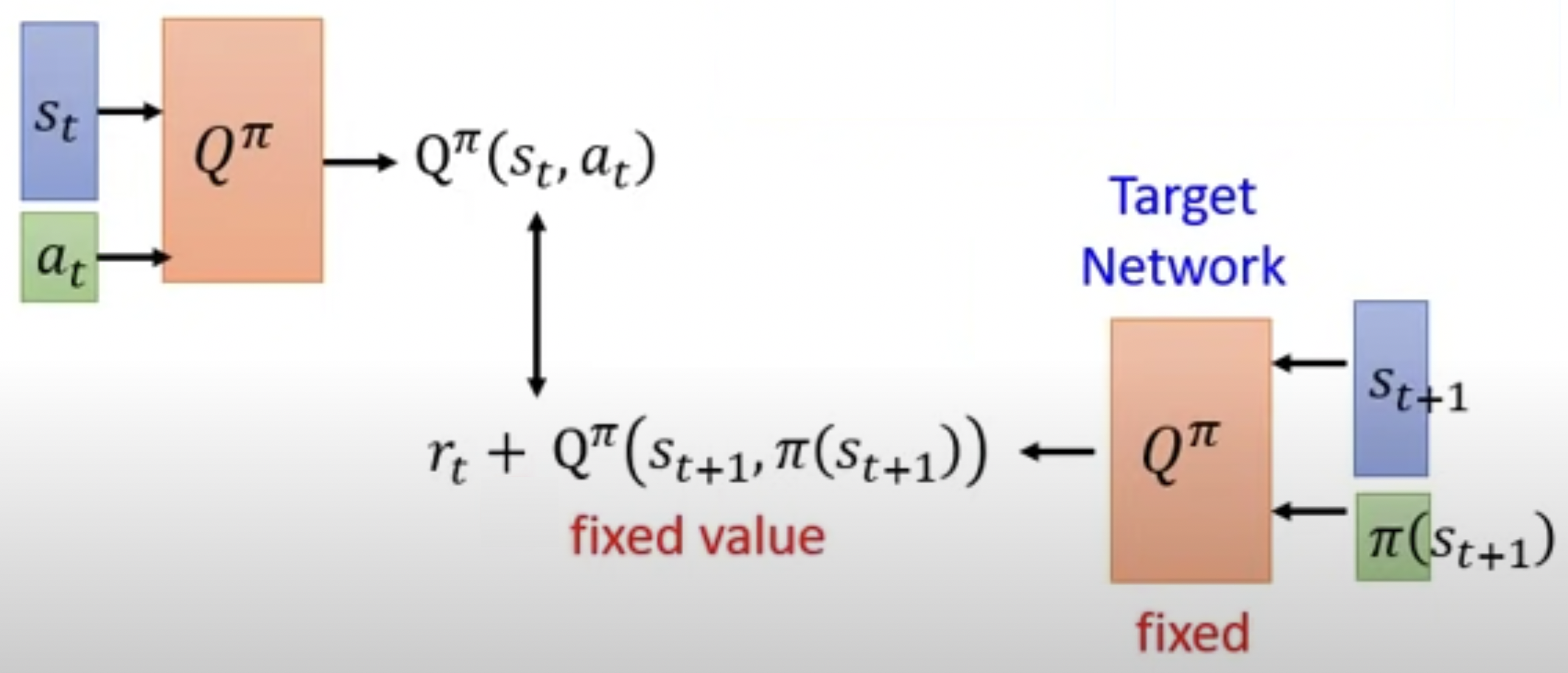
原始的 DQN 使用的是图5的模型结构，将其换一下形式，改成下图6的形式。输入为 (s_t, a_t) 时输出为 Q^\pi(s_t, a_t)；输入为 (s_{t+1}, \pi(s_{t+1})) 时输出为 Q^\pi(s_{t+1}, \pi(s_{t+1}))。将右侧的 model 称为 Target Netword，也就是把 r_t + Q^\pi(s_{t+1}, \pi(s_{t+1})) 当作标签。在原始的 DQN 中由于下图中左右两个模型 Q^\pi 是同一个模型，每一次迭代更新该模型都会变化，所以标签所属的分布也是在随着模型 Q 不断变化的。当标签所属的分布在不断变化时，就会变得非常难以训练。

Target Network 方法所提出的改进就是：在训练左侧的模型 Q^\pi 时，先将右侧的模型冻住不更新，待左侧的模型更新一定的次数之后，使用左侧模型的参数权重覆盖掉右侧模型的参数权重。然后冻住右侧模型，更新左侧模型，按此方法进行迭代训练。在该方法中左右两个模型就不是同一个模型了，在第 4.4 小节描述算法过程时，使用符号 Q 表示下图中左侧的不断进行更新的模型，使用符号 \hat{Q} 表示下图右侧被冻住的模型。

图6

4.2 Exploration#

原始的 DQN 使用下式来获取新的策略 \pi^\prime：

\begin{equation}a = \text{argmax}_a Q(s, a)\end{equation}

这种方法是有问题的。在初始时所有的动作 a 都没有被采样过，也就是说给这些动作的价值的估计值都是0。此时只要采样到任何一个动作 a 的价值是正的，那么之后严格按照上述公式的话，之后就只会选取这个动作了。因为只有这个动作的价值的估计值是正的，其他的动作由于还没有被采样到所以价值的估计值是0。因此，就要求模型不能只选取价值最高的动作，还应该尝试探索更多的工作，基于此有以下两种设计。

4.2.1 Epsilon Greedy#

该方法是把原始 DQN 中的公式 a = \text{argmax}_a Q(s, a) 改为下式：

\begin{equation}a = \begin{cases}\text{argmax}_a Q(s, a) &1-\epsilon \\ \text{random} &\text{other} \end{cases}\end{equation}

该公式的意思是：以 1-\epsilon 的概率选取价值最高的动作，另外的情况随机选取动作。其中 \epsilon 一般是比较小的值，比如：0.1。当然在实际操作中，\epsilon 还可以是随着时间减小的。初始状态时，由于动作价值函数的 model 效果不好估计不准确，分配更大的概率给随机选取动作。随着训练的进行，动作价值函数的 model 变得越来越准，那么就更大的概率使用该 model 选取动作。

4.2.2 Boltzman Exploration#

另外一种方法是，把原始 DQN 中的公式改为下式。新的策略 \pi^\prime 看到状态 s 之后不再是固定采取某个动作 a，而是通过下式计算出每个动作 a 的分布，每次都从该分布中采样出动作 a。对于价值比较高的动作，其采样的概率比较大；对于价值比较低的动作，也有一定的概率被采样到，不会出现永远无法被采样到的问题。

\begin{equation}p(a|s) = \frac{\text{exp}(Q(s,a))}{\sum_a \text{exp}(Q(s,a))}\end{equation}

4.3 Replay Buffer#

先说明这个 Replay Buffer 具体是如何操作的，然后再说明其作用。

首先开辟出一块空间用于存储采样到的数据，这个空间的大小是预先设定好的，如果该空间已经满了，又放入一条数据时，就把最老的那一条数据移除。DQN 的训练流程为：从模型 Q 中依照采样策略采样出一条数据 (s_t, a_t, r_t, s_{t+1}) 之后，就把该条数据放入到该 buffer 中。然后从该 buffer 中随机选取一条数据 (s_i, a_i, r_i, s_{i+1}) 用于学习和更新模型 Q，注意随机选出的这条数据不一定是刚刚放入的那一条数据。当然，在实际操作时每个 step 中可以，从模型 Q 中依照策略采样出一条数据放到 buffer 中，然后从该 buffer 中选取一个 minibatch 的数据（多条数据）用于学习和更新模型 Q。

在 DQN 的训练过程中，这个 buffer 中的数据不一定是当前最新的模型对应的策略采样出来的，有可能是之前旧的模型对应的策略采样出来的。该方法的作用有：

  • 由于这些数据可能是不同阶段的模型对应的策略采样的结果，保证了数据的多样性。经实验证明这种多样性对模型的训练是很有益的；
  • 数据可以多次使用，比如每次采样生成一条新数据放到 buffer 中，然后从 buffer 取出多条数据用于训练；

4.4 DQN 改进算法的算法过程#

下面把上面所述的 Target Network、Exploration、Replay Buffer 三个方法都用上，改进后的 DQN 算法的算法过程如下所示：

  • 初始化 Q-function 的模型，记为 Q；初始化 target Q-function 的模型，记为 \hat{Q}。

  • 循环遍历多个 episode，对于每个 episode：

    • 遍历每个时刻 t：

      • 给定状态 s_t，使用模型 Q，依照下述策略选出动作 a_t：
      a_t = \begin{cases}\text{argmax}_a Q(s_t, a_t) &1-\epsilon \\ \text{random} &\text{other} \end{cases}

      • 有了 s_t 和 a_t 之后，跟环境做交互可以得到 r_t 和 s_{t+1}；

      • 将 (s_t, a_t, r_t, s_{t+1}) 存储到 buffer 中；

      • 从 buffer 中 sample 出数据 (s_i, a_i, r_i, s_{i+1})；（多数情况下会 sample 一个 batch 的数据）

      • 给定状态 s_{i+1}，使用模型 \hat{Q} 依照下述公式遍历所有可能的动作 a，计算出要拟合的目标：

      y = r_i + \text{max}_a \hat{Q}(s_{i+1}, a)

      • 将 (s_i, a_i) 输入到模型 Q 得到 Q(s_i, a_i)；然后就是 Q(s_i, a_i) 作为 logits，y 作为 label，按照 regression 任务对模型 Q 进行优化就可以了；

      • 每过 C 个 step 就用模型 Q 的参数覆盖掉模型 \hat{Q} 的参数。

Reference#