LoRA#

LoRA（Low-Rank Adaptation）已经火了很久了，有了不少的资料，也有不少的代码实现，比如 peft。不过还是按照：读读论文、看看源码、跑跑实验、写写笔记，这几个步骤系统的学习一下这个东西。

本文主要是从 "论文说明"、"代码说明"、"显存与计算量分析" 这三部分介绍一下 LoRA。

1、论文说明#

1.1 本文主要贡献#

提出了一个新的参数高效微调方案：LoRA；
可以对多个不同的任务分别训练多个 LoRA 模块，部署推理时只部署一份主干模型，根据不同的任务使用不同的 LoRA 模块，大大节省显存；
使用 LoRA 做参数高效微调，大幅降低了对显存的需求；（所有参数高效微调方法都有该优势）；
在部署仅用于推理的服务时，可以将 LoRA 模块与主干模型的权重合并，这样不增加任何的推理成本；
LoRA 与许多现有的参数高效微调方法正交，可以结合使用；

论文中提到的这几个 LoRA 的优点，有些是不能够同时做到的。比如上述第2条和第4条之间就是互斥的。第4条是说为了不增加额外的推理时间，将 LoRA 模块的权重与主干模型的权重合并；这样就没有办法实现第2条中所说的只部署一个主干，部署多份 LoRA 模块达到节省显存的目的。总之，节省时间还是节省空间，只能选一个。

1.2 理论说明#

以 Causal Language Model 为例。模型的全量参数使用符号 $\Phi$ 来表示，如果是全量参数微调，那么每次迭代就是 $\Phi := \Phi + \Delta \Phi$ ，等同于是在优化下述公式：

$\begin{equation}\max_{\Phi} \sum_{(x,y) \in Z} \sum_{t=1}^{|y|} \log \big(P_{\Phi} (y_t|x, y_{<t})\big)\end{equation}$

其中 $Z$ 表示整个数据集，每条数据由输入序列 $x$ 和输出序列 $y$ 组成。 $\Phi$ 表示模型中全部的参数， $P\big(y_t|x, y_{<t}\big)$ 就是 Causal Language Modeling 中的预测下一个 token 任务。

以上公式是对模型中的全量参数 $\Phi$ 做微调，当模型非常大时，微调起来很困难。然后就会想到在原始的大量参数的基础上再增加一小部分参数，微调时只微调这一部分参数，在工程上会容易操作很多。这部分参数记为 $\Theta$ ，并且有 $|\Theta| \ll |\Phi|$ ，那么每次迭代就是 $\Phi := \Phi + \Delta \Phi(\Theta)$ ，此时就等同于在优化下述公式：

$\begin{equation}\max_{\Theta} \sum_{(x,y)\in Z} \sum_{t=1}^{|y|} \log \big( p_{\Phi + \Delta \Phi(\Theta)} (y_t | x, y_{<t}) \big)\end{equation}$

符号和上面的公式（1）相同，不再解释。

上述这一段理论说明不只对 LoRA 是适用的，对一些其他的参数高效微调方法也是适用的。

在之前的一些研究结果中表明，尽管预训练模型的参数量很大，但每个下游任务对应的本征维度（Intrinsic Dimension）并不大。所以在训练下游任务时，可以使用非常少的参数量进行微调，来达到一个还不错的效果。

1.3 Approach#

1.3.1 满秩、降秩、低秩#

TODO 这里简单啰嗦一句满秩、降秩、低秩这几个概念，防止忘了。

1.3.2 LoRA 基础说明#

如下图1所示，蓝色框中的矩阵 $W$ 表示预训练模型中的某个全连接层（注意这里必须是一个纯粹的全连接层，而不能是其他的复杂的模型结构），该层的维度是 $d*d$ ，在做微调时这部分的权重冻住不动。右侧由两部分构成，一个全连接层 $A$ 和一个全连接层 $B$ ，全连接层 $A$ 的维度是 $d*r$ ，全连接层 $B$ 的维度是 $r*d$ ，所以这两部分的总参数量为 $2r * d$ ，由于 $r \ll d$ 所以有 $(2r * d) \ll (d * d)$ ，在实际训练时只训练右侧参数量比较少的这两部分。

在前向传播时，数据 $x$ 会同时进入左侧的矩阵 $W$ 与右侧的两个矩阵 $A$ 和 $B$ ，从上述描述的维度可以看出左右两侧输出的结果的隐层维度是相同的，都是 $d$ ，这样就可以直接将左右两侧的输出直接相加得到最终的输出结果。这段描述可以用如下的公式表示：

$\begin{equation}h = Wx + BAx\end{equation}$

然后看一下 $A$ 、 $B$ 、 $W$ 这几个矩阵的关系。矩阵 $A$ 和 $B$ 的维度分别为 $d*r$ 和 $r*d$ ，直接将这两个矩阵相乘可以得到一个维度为 $d*d$ 的权重矩阵，这个维度就跟矩阵 $W$ 的维度完全相同了。只不过由 $A、B$ 相乘得到矩阵的秩是 $r$ ，非常小。

另外，由上述分析可知，当训练完成之后，如果将 $A、B$ 相乘得到的矩阵与 $W$ 相加得到新的矩阵记作 $W^{\prime}$ ，在推理时直接使用矩阵 $W^{\prime}$ 与使用图1中左右两侧分别计算然后再相加得到的结果是完全相同的。即当 $W^{\prime} = W + BA$ 时，则有如下公式：

$\begin{equation}h = W^{\prime}x = Wx + BAx\end{equation}$

这也就是 LoRA 这个方法可以在推理时不增加任何额外开销的原因。

图1

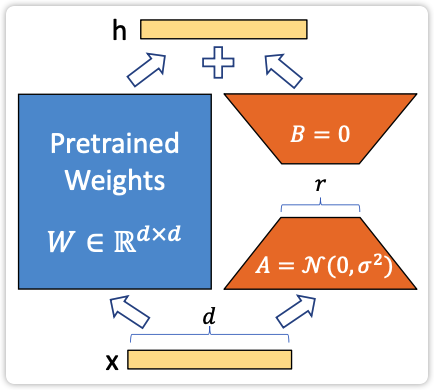关于矩阵 $A$ 和 $B$ 的初始化

对于矩阵 $A$ 使用随机高斯分布初始化，对于矩阵 $B$ 使用全0初始化，这样在初始状态这两个矩阵相乘 $BA$ 的结果为0。这样能够保证在初始阶段时，只有主干分支生效。

在文章梯度视角下的LoRA：简介、分析、猜测及推广中有提到，上述初始化方式带来了不对称问题（一个全零，一个非全零），并提出了一种对称的初始化方式。可以对矩阵 $A$ 和 $B$ 都是使用随机高斯分布初始化，然后在矩阵 $W$ 中减去 $BA$ 就可以保证初始状态时的输出结果与预训练模型是完全一致的。不过如果采用了这种方式，那么在 1.1 小节 "本文的主要贡献" 中，第2条所描述的只部署一个主干，然后部署多份 LoRA 的部署方法就不可用了。

1.3.3 在 transformer 中使用 LoRA#

Transformer 中有 multi-head attention 和 ffn 两部分。其中 multi-head attention 中有四个权重矩阵，分别记为 $W_q$ 、 $W_k$ 、 $W_v$ 、 $W_o$ ，ffn 中有两个权重矩阵。其中 $W_q$ 、 $W_k$ 、 $W_v$ 在实际运算时是多头计算的，这里也直接将其看做维度为 $d_{model}*d_{model}$ 的矩阵。

在本论文中只考虑在 mutil-head attention 中使用 LoRA。至于 ffn 以及模型中的 LayerNorm 部分，使用 LoRA 进行微调能够取得什么效果，没有做研究。

在 transformer 中使用 LoRA 应该说是实际工程中最关心的部分，从以下两个方面来确定使用 LoRA 的细节：

在给定参数量预算的情况下，应该对 transformer 中的哪些层使用 LoRA 可以取得最优效果？（所谓给定参数量预算就是指所有 LoRA 模块加起来的参数量是固定的，因为参数量越多需要的计算资源就越多，所以研究固定参数量情况如何取得最优结果是有必要的）
LoRA 部分的秩 $r$ 如何选取？

1.3.4 给定参数量预算，应该作用到 transformer 哪些层？#

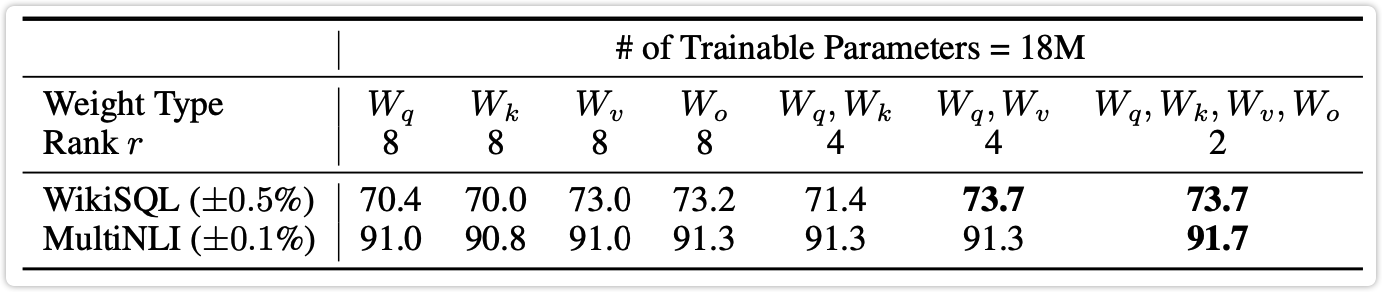
选取的模型是 175B 参数量的 GPT-3 模型，给 LoRA 设定的参数量预算为 18M，然后是对 multi-head attention 中的 $W_q$ 、 $W_k$ 、 $W_v$ 、 $W_o$ 分别进行实验。如果只对这四层中的某一层使用 LoRA 那么秩 $r$ 为8；如果对其中的两层使用 LoRA，那么为了保证参数量不变，此时秩 $r$ 就为4。

实验结果如下表1所示，其中：

前四列分别表示只对 $W_q$ 、 $W_k$ 、 $W_v$ 、 $W_o$ 这四个层中的某一层使用 LoRA 进行训练，秩为8；
第五列表示同时对 $W_q$ 和 $W_k$ 这两层使用 LoRA 进行训练，秩为4；
第六列表示同时对 $W_q$ 和 $W_v$ 这两层使用 LoRA 进行训练，秩为4；
第七列表示同时对 $W_q$ 、 $W_k$ 、 $W_v$ 、 $W_o$ 这四层使用 LoRA 进行训练，秩为2；

可以看出最好的效果是同时对四层使用 LoRA 进行训练，其次是对 $W_q$ 和 $W_v$ 这两层使用 LoRA 进行训练。也就是说相比于对单一的层使用较大的秩，对更多的层使用较小的秩的效果更好。

表1

1.3.5 秩 $r$ 如何选取？#

下表2是探索秩 $r$ 取不同的值时最终的效果。还是在 WikiSQL 和 MultiNLI 这两个任务上做评估，秩的取值选取了 $1、2、4、8、64$ 这五个值。注意在这组实验中肯定就不存在总参数量相同了，不同组实验的总参数量肯定是不同的。

从下表2中可以看出，在任务 WikiSQL 上选取 $r=1$ 同时对 $W_q$ 、 $W_k$ 、 $W_v$ 、 $W_o$ 这四层使用 LoRA 进行训练居然是指标最高的，达到了 $74.1\%$ 。其次是选取 $r=4$ 或 $r=8$ 时指标为 $74.0\%$ 。

在任务 MultiNLI 中，选用 $r=2$ 或 $r=4$ 同时对 $W_q$ 、 $W_k$ 、 $W_v$ 、 $W_o$ 这四层使用 LoRA 进行训练可以得到最优的指标： $91.7\%$ 。

可以看出只需要比较小的秩，比如 $r=4$ 或 $r=8$ ，就已经能够取得比较好的效果。

表2

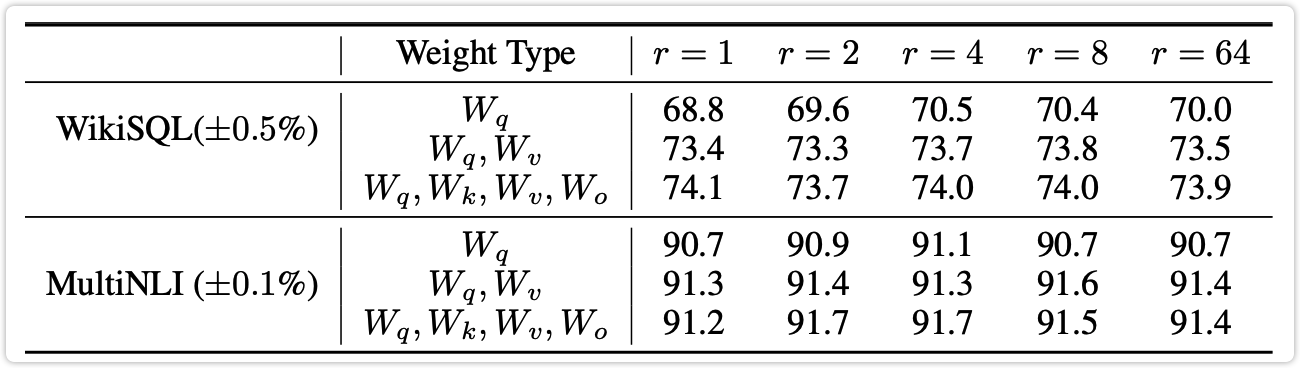由上表可以得到如下结论：

结论1：适配更多的权重矩阵（ $W_o$ , $W_k$ , $W_q$ , $W_v$ ）比适配具有较大秩的单一类型的权重矩阵表现更好。
结论2：增加秩不一定能够覆盖一个更有意义的子空间，一个低秩的适配矩阵可能已经足够了。

2、代码说明#

在整个计算图中，一个 Linear 权重矩阵可以看做是图中的一个节点。项目 peft 中实现 LoRA 的思路是这样的，PyTorch 中的 torch.nn.Linear 表示图1中 "蓝色的矩阵 $W$ "，然后 peft 中自己继承 torch.nn.Linear 实现了一个新的类 LoraLinear，该类表示图1中 "蓝色的矩阵 $W$ "、"橙色的矩阵 $A$ "、以及 "橙色的矩阵 $B$ "，也就是图1中的三个权重矩阵都在 LoraLinear 中实现了。定义了该类之后，只需要在计算图中将对象 torch.nn.Linear 替换为 LoraLinear 就可以了。

以上是 peft 中如何实现 LoRA 的简单说明，下面是细节说明。

这部分的代码都是从 https://github.com/huggingface/peft/blob/v0.3.0/src/peft/tuners/lora.py 中摘取出来的。这里的目的是整体了解一下 LoRA，所以下述代码做了部分的删减和改写。

2.1 自定义的 `LoraLinear` 类#

自定义一个 LoraLinear 类，该类是在 PyTorch 的 torch.nn.Linear 的基础上增加 LoRA 的功能，下面分别说明该类的初始化和前向传播过程。在项目 peft 中这个类的名字叫 Linear，在这里为了和 torch.nn.Linear 做区分，这里使用名字 LoraLinear。

在 LoraLinear 中有两部分功能，一部分是其父类 torch.nn.Linear 的功能，另一部分是新增的 LoRA 的功能。其父类的功能这一块比较清晰，因为都是 torch.nn.Linear 的功能，在代码中有两个地方体现：

在 __init__ 函数中调用其父类的init函数做初始化；
使用 LoraLinear 替换模型中原始 torch.nn.Linear 时，将原始的线性层的权重赋值给 LoraLinear，对应的代码为 new_module.weight = old_module.weight，这部分操作的细节在下面的 2.2 使用 LoRA 对象替换原对象 小节；

另一部分功能是新增的 LoRA 的功能，其在代码中的体现主要是初始化部分和前向传播部分。初始化部分好说，如下述代码，直接将 LoRA 相关的配置存储起来即可。

class LoraLinear(nn.Linear):

    def __init__(self, in_features: int, out_features: int):
        nn.Linear.__init__(self, in_features, out_features, **kwargs)
        self.r = ...
        self.lora_alpha = ...
        self.scaling = ...
        self.lora_dropout = ...
        self.lora_A = ...
        self.lora_B = ...

        self.in_features = in_features
        self.out_features = out_features
        ... ...

下面是前向传播的代码，核心就是三部分：主干模型做前向传播、LoRA 模型做前向传播、将两部分前向传播结果相加。在下面的代码块中，每行代码和注释的对应关系是比较清晰的。然后是对应一下代码和公式之间的关系：

代码中的 result 就是公式中的 $Wx$ ；
代码中的 lora_result 就是公式中的 $BAx$ ；
代码中的 final_result 就是将上述两个结果相加，即 $h = Wx + BAx$ ；

class LoraLinear(nn.Linear):

    def forward(self, x: torch.Tensor):
        ... ...

        # 这个就是执行的 torch.nn.Linear 的功能，对应的模型结构就是主干部分的模型结构；
        result = F.linear(x, transpose(self.weight, self.fan_in_fan_out), bias=self.bias)

        x = x.to(self.lora_A.weight.dtype)

        # 这一部分是 LoRA 部分的模型结构；
        # 可以看出主干部分和 LoRA 部分的输入是相同的，都是 x
        lora_result = self.lora_B(self.lora_A(self.lora_dropout(x))) * self.scaling

        # 将主干部分的输出和 LoRA 部分的输出直接相加作为最终输出
        final_result = result + lora_result
        ... ...

2.2 使用 LoRA 对象替换原对象#

使用上一小节中自定义的 LoraLinear 这个对象替换模型中的 torch.nn.Linear 对象。主要的步骤如下述代码所示，说明都放在注释中了：

# 获取想要使用 LoRA 训练的层的信息。这里的 key 和 module_name 是有区别的，举例说明：
#   比如 key 为 transformer.layers.0.attention.query，那么 module_name 为 query
parent_module, old_module, module_name = _get_submodules(model, key)

# 创建一个自定义的带有 LoRA 功能的对象：LoraLinear
in_features, out_features = old_module.in_features, old_module.out_features
new_module = LoraLinear(in_features, out_features, bias=bias, **kwargs)

# 用上述创建的自定义的对象替换原来的模型层
setattr(parent_module, module_name, new_module)  # 更换计算图中的节点
new_module.weight = old_module.weight
if getattr(old_module, "state", None) is not None:
    new_module.state = old_module.state
    new_module.to(old_module.weight.device)

2.3 项目peft中LoraConfig参数介绍#

r: lora的秩，矩阵A和矩阵B相连接的宽度， $r \ll d$ ；
lora_alpha: 归一化超参数，lora参数 $\Delta Wx$ 会以 $\frac{\alpha}{r}$ 归一化，以便减小改变 $r$ 时需要重新训练的计算量；
lora_dropout: lora层的dropout比率；
merge_weights: eval模式，是否将lora矩阵的值加到原有 $W_0$ 的值上；
fan_in_fan_out: 只有应用在 Conv1D 层时置为True，其他情况为False；
bias: 是否可训练bias；
modules_to_save: 除了lora部分外，还有哪些层可以被训练，并且需要保存；

3、显存与计算量分析#

3.1 显存分析#

在训练时，都有哪些消耗显存的部分，可见之前的文章参数量估计与显存估计，下面基于此分析使用 LoRA 训练时的显存消耗。

主干模型部分：

首先主干模型的权重都要存储到显存中，这部分显存无法省掉。

其次，虽然只对 LoRA 部分的模型进行优化，但是想要求 LoRA 部分的梯度，那么主干的梯度也是必须要求解出来的，所以主干模型的梯度是必须要求的。

由于不需要优化主干模型，所以主干模型对应的优化器不需要存储，这部分显存可以节省调。

LoRA 模型部分：

LoRA 模型的权重、梯度、优化器状态都需要存储，这个是没有疑问的。

结论：LoRA 在显存方面就只是节省了主干模型的优化器状态。

另外，在实际使用中，由于主干模型不需要优化，所以这部分可以使用fp16，甚至 int8、int4 量化，也会显得显存消耗大幅减小。

3.2 计算量分析#

涉及到计算的主要分为前向传播、反向传播、优化器更新权重，这三部分。下面也主要是看这三部分中哪部分可以省掉。