[隐藏左侧目录栏][显示左侧目录栏]

马尔可夫随机过程、奖励过程、决策过程#

重要！！！

涉及到马尔可夫过程，就必须要强调的两个概念：一个概念是所有状态的集合，一个概念是时间序列。

  • 所有状态的集合使用数学符号 \mathcal{S} = \{s_1, s_2, ..., s_n\}，其表示可以取到的状态值。在本文中其下标一般使用 n，表示总共有 n 个状态值。

  • 时间序列使用数学符号 (S_1, S_2, ..., S_t, ..., S_T)，其表示从初始时刻开始到 T 时刻做了一次采样之后得到的结果。在本文中其下标一般使用 t，表示在第 t 时刻所取到的状态。

在本文中，表示某一个状态值时使用小写的 s 来表示，表示某个时刻的状态时使用大写的 S 来表示。

刚开始看马尔可夫过程时，对这两个概念弄混了很久。

1、随机过程#

概率论的研究对象是静态的随机对象。随机过程（stochastic process）的研究对象是随时间演变的随机对象。

在随机过程中，某一时刻 t 的状态取值使用符号 S_t 表示（这里的 s 是单词 state 的首字母），所有可能的状态的集合使用符号 \mathcal{S} = \{s_1, s_2, ..., s_n\} 表示。

某个时刻 t 的状态取决于之前各个时刻的状态，也就是说，已知 (S_1, S_2, ..., S_t)，那么下一时刻 t+1 的状态 S_{t+1} 的概率表示为 P(S_{t+1}|S_1, S_2, ..., S_t)。

2、马尔可夫随机过程(MP)#

2.1 马尔可夫性质#

马尔可夫性质（Markov property）：某一时刻的状态仅取决于上一时刻的状态，用公式表示为 P(S_{t+1}|S_t) = P(S_{t+1}|S_1, S_2, ..., S_t)。

2.2 马尔可夫随机过程#

马尔可夫过程（Markov process）也称为马尔可夫链（Markov chain），指的是具有马尔可夫性质的随机过程。一般使用符号 <\mathcal{S}, \mathcal{P}> 表示。其中 \mathcal{S} 表示 有限个 状态的集合，\mathcal{P} 表示状态转移矩阵（state transition matrix）。

假设总共有 n 个状态，此时 \mathcal{S} 和 \mathcal{P} 的公式分别如下所示：

\begin{equation}\mathcal{S}=\{s_1, s_2, ..., s_n\}\end{equation}
\begin{equation}\mathcal{P}=\begin{bmatrix} P(s_1|s_1) & P(s_2|s_1) & \cdots & P(s_n|s_1) \\ \vdots & \vdots & \ddots & \vdots \\ P(s_1|s_n) & P(s_2|s_n) & \cdots & P(s_n|s_n) \end{bmatrix}\end{equation}

上述状态转移矩阵 \mathcal{P} 中第 i 行第 j 列的元素 P(s_j|s_i) 表示从状态 s_i 转移到状态 s_j 的概率。

从任一状态出发，转移到所有状态的概率之和必须为1，所以在状态转移矩阵 \mathcal{P} 中每一行元素之和为1。

对于那些只进不出的状态（在状态转移矩阵 \mathcal{P} 中表现为以1的概率转移到自身），一般称其为终止状态（terminal state）。

给定了 \mathcal{S} 和 \mathcal{P} 之后就意味着给定了马尔可夫过程。给定了一个马尔可夫过程之后，就可以从某一个状态出发，根据其状态转移矩阵生成一个状态序列（episode）。这种操作一般称为采样（sampling）。

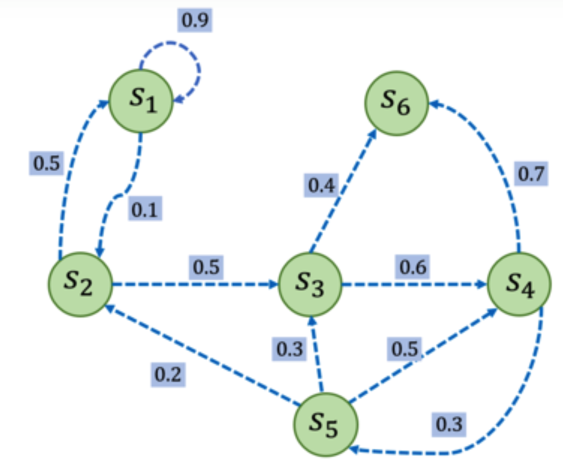
下图就是一个马尔可夫过程的例子，下图中的每个点就是一个状态，每个边对应着状态转移矩阵中的一个元素（转移概率为0的都省略了没有画出来）。可以看出下图中的 s6 节点只进不出，所以其就是一个终止节点。

3、马尔可夫奖励过程(MRP)#

3.1 奖励过程#

马尔可夫奖励过程（Markov reward process）就是在马尔可夫过程的基础上增加上奖励函数 r 和折扣因子 \gamma。

某个状态的奖励函数 r(s) 指的是转移到该状态可以获得的奖励的期望。

折扣因子（discount factor） \gamma 的取值范围是 [0, 1)。引入折扣因子的作用是长期的奖励具有一定的不确定性，折扣因子的作用就是对长期的奖励打一个折扣、做一个衰减，更关注近期的奖励。\gamma 越接近0说明越忽略长期奖励，\gamma 越接近1说明越关注长期奖励。折扣因子是在计算下一小节所讲的 "回报" 时起的作用。

所以，一个马尔可夫奖励过程可以使用符号 <\mathcal{S}, \mathcal{P}, r, \gamma> 来表示。

另外，使用符号 R_t 表示在 t 时刻获得的奖励。举例说明一下奖励函数 r(s) 与奖励 R_t 的区别。假设对于某个状态 s 其有0.8的概率获取1点奖励，有0.2的概率获得5点奖励。那么某次采样可能得到1点奖励，此时 R_t=1，另一次采样可能得到5点奖励，此时 R_t=5。而其奖励函数表示的是该状态可以获得的奖励的期望，永远为 r(s)=0.8*1+0.2*5=1.8。也就是说，奖励函数 r(s) 是不随时刻 t 变化、不随采样次数变化的；而奖励 R_t 则是某次采样的具体结果。

3.2 回报#

在马尔可夫奖励过程中，从 t 时刻的状态 S_t 开始，直到终止状态，所有奖励的衰减之和称为回报，使用符号 G_t 表示。其公式为：

\begin{equation}G_t = R_t + \gamma R_{t+1} + \gamma ^ 2 R_{t+2} + \cdots = \sum_{k=0}^\infty \gamma^k \cdot R_{t+k} \end{equation}

其中 \gamma 是折扣因子，R_t 是在 t 时刻获得的奖励，都在上一小节介绍过了。

3.3 价值函数#

在马尔可夫奖励过程中，一个状态的期望回报（即从这个状态开始未来累积奖励的期望）称为这个状态的价值（value），所有状态的价值就构成了期望函数（value function），其公式为：

\begin{equation}V(s) = E[G_t|S_t=s]\end{equation}

3.4 贝尔曼方程#

3.4.1 贝尔曼方程推导#

从上述价值函数出发，可以推导出贝尔曼方程（Bellman equation），推导过程如下所示：

\begin{equation}\begin{split} V(s) &= E[G_t|S_t=s] \\ &= E[R_t + \gamma R_{t+1} + \gamma^2 R_{t+1} + \cdots | S_t = s] \\ &= E[R_t + \gamma (R_{t+1} + \gamma R_{t+1} + \cdots) | S_t = s] \\ &= E[R_t + \gamma G_{t+1} | S_t = s] \\ &= E[R_t + \gamma V(R_{t+1}) | S_t = s] \end{split}\end{equation}

上述推导过程的最后一行在刚开始看的时候完全无法理解，主要不理解的是为什么能够对价值函数 V(R_{t+1}) 求期望，也就是公式 E[V(R_{t+1})] 是什么意思？这里专门对最后一行的含义做一下解释。

公式中的 [|S_t=s] 意思是在时刻 t 状态为 s。公式中的 R_t 表示在时刻 t 获得的奖励。最主要是公式中的 E[V(R_{t+1})] 的含义是什么。

从之前的定义已经知道 V(s) 表示的是当前时刻 t 的状态为 s，从当前时刻到序列结束所获得的所有回报 G 的期望。在该定义中非常重要的一点是：当前时刻 t 的状态是固定的，就是状态 s，而不是状态集合 \mathcal{S} 中任何其他的状态。假设现在只知道时刻 t 是状态 s，对于时刻 t+1 以及之后的时刻是什么状态都是未知的，那么如何表示从时刻 t+1 直到序列结束所获得的所有回报的期望呢？可以遍历 t+1 时刻的所有可能的状态，求出每个状态的价值，然后就可以求出期望了，这个过程使用公式表示就为：E[V(R_{t+1})]=\sum_{s^\prime \in \mathcal{S}} p(s^\prime) V(s^\prime)。所以符号 E[V(R_{t+1})] 的含义是：在不知道 t+1 时刻是什么状态的情况下，从 t+1 时刻到序列结束所获得的所有回报 G 的期望。

然后根据上述推导过程的最后一行就有了贝尔曼方程，公式如下：

\begin{equation}V(s) = r(s) + \gamma \sum_{s^\prime \in S} p(s^\prime | s) V(s^\prime)\end{equation}

3.4.2 贝尔曼方程直观理解#

从形式上来看，贝尔曼方程其实是状态 s 的价值和其下一个状态 s^\prime 的价值的递归式。下面从直观上说明一下贝尔曼方程表示的意思。等号左侧是状态 s 的价值，它等于两部分求和。一部分是当前状态 s 的奖励期望，另一部分是衰减后的下一状态 s^\prime 的价值的加权和。加权和中的权重就是状态 s 转移到状态 s^\prime 的概率。

对于状态集合 \mathcal{S} 中的任何一个状态 s，贝尔曼方程都是成立的。

3.4.3 贝尔曼方程矩阵形式#

下面把贝尔曼方程写成矩阵形式。假设马尔可夫奖励过程有 n 个状态，即 \mathcal{S} = \{s_1, s_2, ..., s_n\}，将所有状态的价值表示成一个列向量 \mathcal{V} = [V(s_1), V(s_2), ..., V(s_n)]^\top，把奖励函数也表示成一个列向量 \mathcal{R} = [r(s_1), r(s_2), ..., r(s_n)]^\top，然后就有贝尔曼方程的矩阵形式：

\begin{equation}\mathcal{V} = \mathcal{R} + \gamma \mathcal{P} \mathcal{V}\end{equation}
\begin{equation} \begin{bmatrix} V(s_1) \\ V(s_2) \\ \vdots \\ V(s_n) \end{bmatrix} = \begin{bmatrix} r(s_1) \\ r(s_2) \\ \vdots \\ r(s_n) \end{bmatrix} + \gamma \begin{bmatrix} P(s_1|s_1) & P(s_2|s_1) & \cdots & P(s_n|s_1) \\ P(s_1|s_2) & P(s_2|s_2) & \cdots & P(s_n|s_2) \\ \vdots & \vdots & \ddots & \vdots \\ P(s_1|s_n) & P(s_2|s_n) & \cdots & P(s_n|s_n) \end{bmatrix} \begin{bmatrix} V(s_1) \\ V(s_2) \\ \vdots \\ V(s_n) \end{bmatrix} \end{equation}

在公式（7）中 \mathcal{R}、\mathcal{P}、\gamma 都是已知量，只有 \mathcal{V} 是未知的，所以这里是可以直接求解其解析解的，做一下简单的变形即可，如下所示：

\begin{equation}\begin{split} \mathcal{V} &= \mathcal{R} + \gamma \mathcal{P} \mathcal{V} \\ (I - \gamma \mathcal{P}) \mathcal{V} &= \mathcal{R} \\ \mathcal{V} &= (I - \gamma \mathcal{P})^{-1} \mathcal{R} \end{split}\end{equation}

根据上式就可以通过 \mathcal{R}、\mathcal{P}、\gamma 求解出 \mathcal{V}，这种方法的时间复杂度为 O(n^3)，其中 n 是状态的个数，因此只有当 n 比较小时才能够使用这种方法，否则的话就太慢了。

4、马尔可夫决策过程(MDP)#

4.1 决策过程#

马尔可夫决策过程（Markov decision process）一般使用 <\mathcal{S}, \mathcal{A}, \mathcal{P}, r, \gamma> 来表示。其中 \mathcal{S} 表示有限个状态的集合，\mathcal{A} 是动作的集合，\gamma 是衰减因子。

r(s, a) 是奖励函数，注意此时的奖励函数既跟 s 有关，也跟 a 有关。

P(s^\prime|s, a) 是状态转移函数，其含义是在状态 s 执行动作 a 之后达到状态 s^\prime 的概率。在马尔可夫决策过程这里已经不再使用状态转移矩阵了，而是使用状态转移函数，这个更具有通用性。

4.2 策略#

智能体的策略（policy）使用符号 \pi 来表示，即：\pi(a|s) = P(A_t=a|S_t=s)，其含义是在状态 s 下采取动作 a 的概率。

确定性策略（deterministic policy）指每个状态确定对应一个动作。

随机性策略（stochastic policy）指在每个状态时，采取哪个action是一个概率分布。在该概率分布中进行采样之后会得到一个具体的状态。

4.3 状态价值函数#

对于马尔可夫决策过程，其奖励函数为 r(s, a)，可以看出其既与 s 有关，也与 a 有关，所以其价值函数也是有两个，分别是这一小节的状态价值函数和下一小节的动作价值函数。

状态价值函数（state-value function）使用符号 V^\pi(s) 表示，定义是从状态 s 出发遵循策略 \pi 所能获得的回报的期望。公式为：

\begin{equation}V^\pi(s) = E_\pi[G_t|S_t=s]\end{equation}

4.4 动作价值函数#

动作价值函数（action-value function）使用符号 Q^\pi(s,a) 表示，定义是在遵循策略 \pi 时，对当前状态 s 执行动作 a 之后，所能获得的回报的期望。公式为：

\begin{equation}Q^\pi(s, a)=E_\pi[G_t|S_t=s, A_t=a]\end{equation}

然后看下状态价值函数 V^\pi(s) 与动作价值函数 Q^\pi(s, a) 之间的转换关系公式：

\begin{equation}V^\pi(s)=\sum_{a \in \mathcal{A}} \pi(a|s)Q^\pi(s, a)\end{equation}
\begin{equation}Q^\pi(s, a)=r(s,a) + \sum_{s^\prime \in \mathcal{S}}P(s^\prime|s,a)V^\pi(s^\prime)\end{equation}

4.5 贝尔曼期望函数#

还是要记着贝尔曼期望函数就是价值函数的递归式。那么，作为递归式，状态价值函数的贝尔曼期望函数就是 V^\pi(s) 与 V^\pi(s^\prime) 的关系。动作价值函数的贝尔曼期望函数就是 Q^\pi(s,a) 与 Q^\pi(s^\prime, a^\prime) 的关系。

状态价值函数的贝尔曼期望函数公式如下：

\begin{equation}V^\pi(s)=\sum_{a\in \mathcal{A}} \pi(a|s) \Big[r(s,a) + \gamma \sum_{s^\prime \in \mathcal{S}} P(s^\prime|s,a)V^\pi(s^\prime) \Big]\end{equation}

动作价值函数的贝尔曼期望函数公式如下：

\begin{equation}Q^\pi(s,a) = r(s,a) + \gamma \Big[ \sum_{s^\prime \in \mathcal{S}} P(s^\prime|s,a) \sum_{a^\prime \in \mathcal{A}} \pi(a^\prime|s^\prime) Q^\pi(s^\prime, a^\prime) \Big]\end{equation}

关于这两个贝尔曼期望方程的直观理解，和第 3.4 部分对贝尔曼方程的直观说明是基本相似的。

Reference#