[隐藏左侧目录栏][显示左侧目录栏]

Actor-Critic#

1、Policy Gradient 回顾#

在 policy gradient 中，求解梯度使用的是下式：

\begin{equation}\nabla \bar{R}_{\theta} = \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \Big( \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n - b \Big) \nabla \text{log}p_{\theta}(a_t^n|s_t^n)\end{equation}

在上述公式中 \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n 这一项表示的是给定状态 s_t^n 之后策略采取了动作 a_t^n 所能够获取到的回报G。减去 b 的作用是让括号里的这一项有正有负。

另外还把 \Big( \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n - b \Big) 这一项使用符号 A^n(s_t^n, a_t^n) 表示，称为 advantage function。

在之前的内容中已经讨论过了，梯度公式中的 \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n 这一项，也就是回报 G 的方差非常大，方差大就导致训练起来非常困难。而如果这里使用回报 G 的期望替代的话，就不会有方差太大的问题了。

之前介绍的 Q-learning 方法就是在估计价值函数，而价值函数的定义正是回报 G 的期望，所以就会想到使用 Q-learning 方法替换掉这里的 \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n。

2、Actor-Critic#

2.1 Actor-Critic#

先来回顾一下之前的价值函数的公式和其含义。

动作价值函数的公式如下，其含义为给定了某个状态且策略采取了某个动作之后，所获得的回报 G 的期望：

\begin{equation}Q^\pi(s, a) = E_{\pi}[G_t|s_t=s,a_t=a]\end{equation}

状态价值函数的公式如下，其含义为给定了某个状态之后，所获得的回报 G 的期望：

\begin{equation}V^{\pi}(s) = E_{\pi}[G_t|s_t=s]\end{equation}

状态价值函数与动作价值函数的转换公式如下，在这里状态价值函数可以看作是动作价值函数的期望：

\begin{equation}V^{\pi}(s) = \sum_{a\in A} \pi(a|s) Q^\pi(s, a) = E_{a \in A}[Q^\pi(s, a)]\end{equation}

当然状态价值函数和动作价值函数之间的转换关系还有下式，不过在这里没有使用到这个公式：

\begin{equation}Q^\pi(s, a) = r(s,a) + \sum_{s^\prime \in S} p(s^\prime | s, a) V^\pi(s^\prime) = E_{s^\prime \in S} \Big[r(s, a) + V^\pi(s^\prime) \Big]\end{equation}

接下来就可以分析一下了。在公式（1）中的 \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n，也就是回报 G 的方差较大，想替换为期望，而动作价值函数的公式（2）就是给定了某个状态且策略采取了某个动作之后，所获得的回报 G 的期望。所以这里可以使用动作价值函数替换掉 \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n。然后在公式（1）中还有减去 b 这么一个操作，在之前的讨论中 b 一般是 \sum_{t^\prime=t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n 的期望，这样能够保证减去 b 之后有正有负，现在替换成动作价值函数 Q^\pi(s, a) 之后，这里的 b 就最好是 Q^\pi(s, a) 的期望。由公式（4）可以看出状态价值函数 V^\pi(s) 就可以看作是动作价值函数的期望，所以这里的 b 就采取状态价值函数。替换完之后的梯度公式如下：

\begin{equation}\nabla \bar{R}_{\theta} = \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \Big[ Q^\pi(s_t^n, a_t^n) - V^\pi(s_t^n) \Big] \nabla \text{log} p_{\theta}(a_t^n|s_t^n)\end{equation}

这个公式就是结合了"基于策略的算法"与"基于值的算法"之后的结果。

2.2 A2C#

A2C 的全称为 Advantage Actor-Critic，就是 Actor-Critic 的改进版。公式（6）里面用到了两个价值函数：Q^\pi 和 V^\pi，也就对应着两个模型。再加上 actor 对应的模型，总共需要训练三个模型。模型越多，系统越复杂，也就越难以训练，所以这里考虑对两个价值函数变形，最终使用一个价值函数实现。

上一小节里面的公式（5）是动作价值函数与状态价值函数之间的转换关系，在这里主要是利用该公式。利用该公式将公式（6）中的 Q^\pi(s_t^n, a_t^n) 部分做如下的一些转换：

\begin{equation}\begin{split} Q^\pi(s_t^n, a_t^n) &= E \Big[ r_t^n + V^\pi (s_{t+1}^n) \Big] \\ &\rightarrow r_t^n + V^\pi (s_{t+1}^n) \end{split}\end{equation}

上述公式中的第一行就是由公式（5）得到的，这个不需要解释。第二行就不是恒等变换了，所以上面使用箭头来表示。箭头的左侧是一个期望，箭头的右侧是直接把期望符号去掉了，等于是某次采样值。使用单次采样值替换掉原来的期望值从理论上来说是近似相等的，它带来的问题是原来的期望值是比较稳定的，而采样值则是随机变量，相比起期望值就没有那么的稳定了。使用期望值的话，方差可以看作是0，而使用随机变量的话，方差肯定是大于0的。

将公式（7）带入到公式（6）里面之后得到新的梯度计算公式：

\begin{equation}\nabla \bar{R}_{\theta} = \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} \Big[ r_t^n + V^\pi (s_{t+1}^n) - V^\pi(s_t^n) \Big] \nabla \text{log} p_{\theta}(a_t^n|s_t^n)\end{equation}

使用该公式就只需要一个模型来估计价值函数，以及一个 actor 对应的模型，总共需要训练两个模型，比之前少了一个。

关于这个改进，单从理论上来说，它的优点是将原来需要训练3个模型的系统简化为了需要训练2个模型的系统；它的缺点是将原来的期望变为了随机变量，也就是公式（7），这增加了训练的难度。所以从理论上来看不能完全说该改进一定有效。但是实验结果胜于理论，经过大量实验证明，经过该改进之后，最终训练出来的模型的效果是要明显优于改进之前的。

2.3 一些其他说明#

上面在介绍 Actor-Critic 方法时，是在"基于策略的算法"上引出来的。首先，有一个基于策略的方法，比如 policy gradient，该方法的梯度公式中需要求解回报 G 的期望，该值不容易直接求解，于是使用一个模型来估计该值。从这个角度来看，Actor-Critic 更像是一个基于策略的方法。

其实 Actor-Critic 还可以从另一个角度进行理解。首先，有一个基于值的算法，比如 DQN，该方法能够估计出一个动作价值函数。有了动作价值函数之后，只需要按照公式 a=\text{argmax}_a Q^\pi(s, a) 就可以获得策略 \pi 了，但是这个公式直接求解不好求，于是使用一个模型（也就是 actor 模型）来对该式进行求解。从这个角度来看，Actor-Critic 更像是一个基于值的方法。

总体来说，Actor-Critic 是结合了基于策略的算法和基于值的算法的，是目前来说效果最好的强化学习方案。

2.4 A2C 算法过程#

算法过程简述如下：

  • 使用策略 \pi（也就是 actor 模型）与环境互动采样数据；

  • 使用上一步采样到的数据 (s_t, a_t, r_t, s_{t+1}) 训练更新 critic 模型；

  • 使用 critic 模型计算出的 advantage 训练更新 actor 模型；

这里记录几个之前一直存在疑惑的点：

  • critic 模型训练时的监督信号是由环境提供的。无论策略 \pi 选出来的策略是好的还是坏的，环境对其的反馈 r_t 是完全准确的，critic 模型拟合的是这个 r_t。所以，在训练 critic 模型时，策略 \pi 仅提供一个动作 a，至于这个策略是否是最优的，从理论上来说对于 critic 模型的训练是没有影响的；

  • actor 模型训练时的监督信号是由 critic 模型提供的。

总体来说：环境提供监督信号用于训练 critic 模型，然后 critic 模型提供监督信号用于训练 actor 模型。

3、A3C#

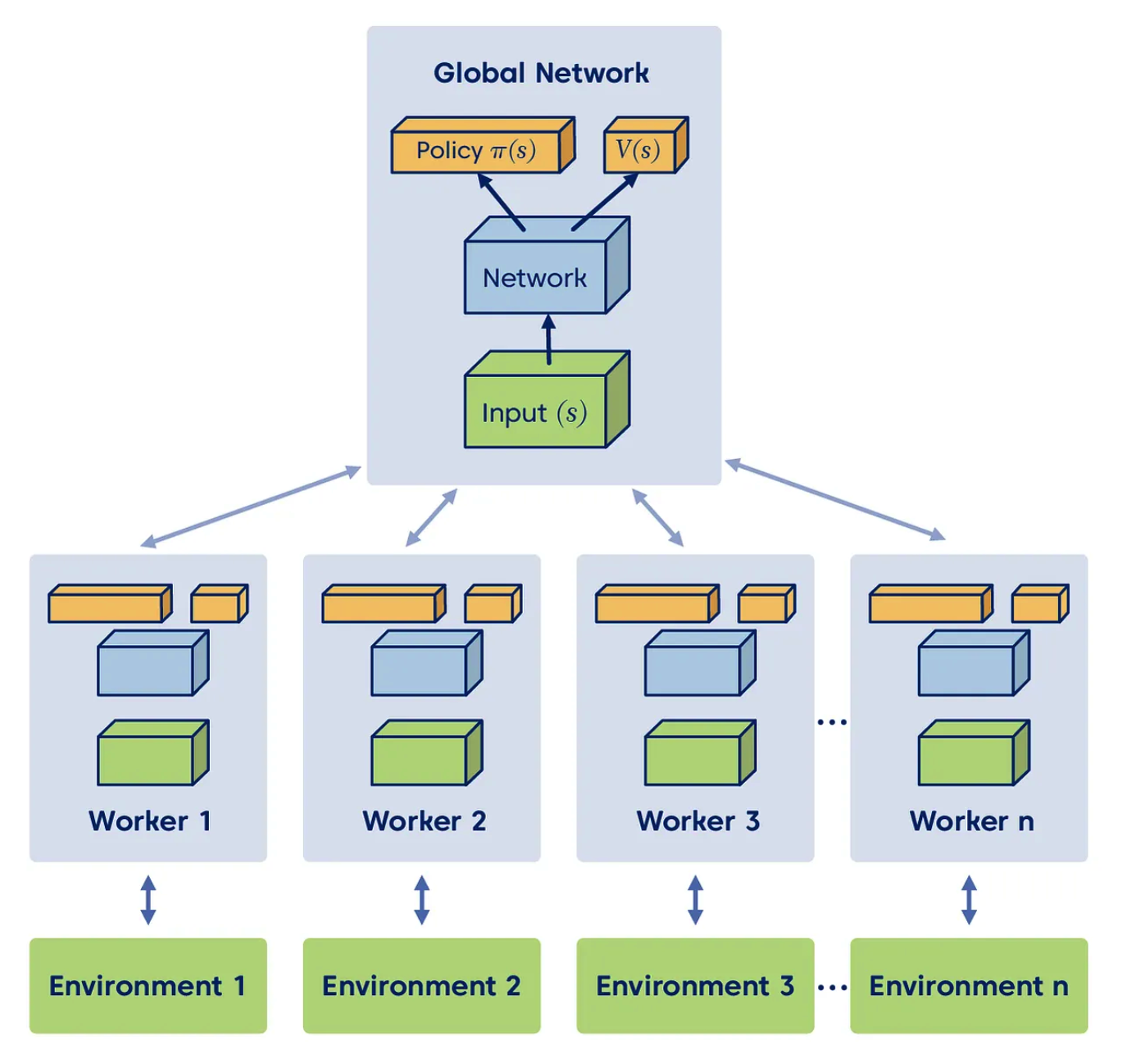
A3C 的全称为 Asynchronous Advantage Actor-Critic，这里的 Asynchronous 是异步的意思。如下图所示，首先有一个 global network，然后有多个 worker。每个 worker 把所有的模型的权重从 global network 那里拷贝出来一份，然后自己就开始进行训练流程：自己采样数据，自己计算梯度。当 worker 计算出来梯度之后，就把这个梯度传给 global network，然后 global network 就使用这个梯度更新自己的模型的权重，更新完成之后，worker 再从 global network 这里拷贝所有的模型的权重，如此往复。

注意，worker 是有多个的，所以对于某一个 worker 来说，它一开始拷贝了一份模型的权重出来，等到计算出梯度之后已经过去一段时间了，此时 global network 的权重可能已经被其他的 worker 回传的梯度更新过了，但是没有关系，不用管这个，还是将 worker 计算出的梯度直接作用到当前的 global network 的参数上。猜测这种操作的原因：一个原因是这样操作简单，另一个原因估计还是为了增加多样性和鲁棒性。

Reference#