Layer Normalize#

1、LN的具体操作步骤#

1.1 简单描述#

layer norm 的计算过程大概有如下几步：

求每条数据各特征之间的均值和标准差；
每条数据的每个特征减去各自数据的均值，除上各自数据的标准差；
对经过上一步骤的输出再经过一个线性变换；

然后使用公式严谨的描述一下 layer norm 的计算过程。

1.2 LN的公式描述#

假设 LN 的输入为 $m$ 条样本，每条样本为一个 $n$ 维的向量。则输入数据的集合表示为： $D = \{\vec{x_1}, \vec{x_2}, ..., \vec{x_m}\}$ ，其shape为 $(m, n)$ 。其中 $\vec{x_i} = [x_i^{(1)}, x_i^{(2)}, ..., x_i^{(j)}, ..., x_i^{(n)}]$ ，右上角的 $\cdot^{(j)}$ 表示该条数据的第 $j$ 个特征；

LN 输出的shape与输入是完全相同的，记为 $\{\vec{y_1}, \vec{y_2}, ..., \vec{y_m}\}$ ，其shape也为 $(m, n)$ 。其中 $\vec{y_i} = [y_i^{(1)}, y_i^{(2)}, ..., y_i^{(j)}, ..., y_i^{(n)}]$ ；

则 LN 的公式如下所示：

$\begin{equation}\begin{split} &\mu_i = \frac{1}{T} \sum_{j=1}^{T} x_i^{(j)} \qquad//\text{第 i 条数据各特征的均值} \\ &\sigma_i^2 = \frac{1}{T} \sum_{j=1}^{T} (x_i^{(j)} - \mu_i)^2 \qquad//\text{第 i 条数据各特征的方差 } \\ &\hat{x_i^{(j)}} = \frac{x_i^{(j)} - \mu_i}{\sqrt{\sigma_i^2 + \epsilon}} \qquad//\text{减去均值，除上标准化，} \epsilon \text{用于避免除数为0} \\ &y_i^{(j)} = \gamma^{(j)} \hat{x_i^{(j)}} + \beta ^{(j)} \qquad//\text{第 i 条数据第 j 个特征经过LN后的结果} \end{split}\end{equation}$

上述最后一个公式的线性变换，是每个特征对应一个 $\gamma$ 和 $\beta$ 。在该分析中，由于每条样本有 $n$ 个特征，所以这个的 $\gamma$ 和 $\beta$ 各有 $n$ 个。不同样本的同一个特征共享相同的 $\gamma$ 和 $\beta$ 。

在 PyTorch 的官方文档中给出的公式为下面形式，虽然符号上有些差异，但是本质是相同的：

$\begin{equation}\hat{x} = \frac{x-E[x]}{\sqrt{Var[x]+\epsilon}} * \gamma + \beta\end{equation}$

1.3 图像描述#

LN的操作还可以用如下图来表示。其中 "-"、"/"、" $\times$ "、"+" 就是常规的减法、除法、乘法、加法。 $Avg$ 是均值， $Std$ 是标准差。

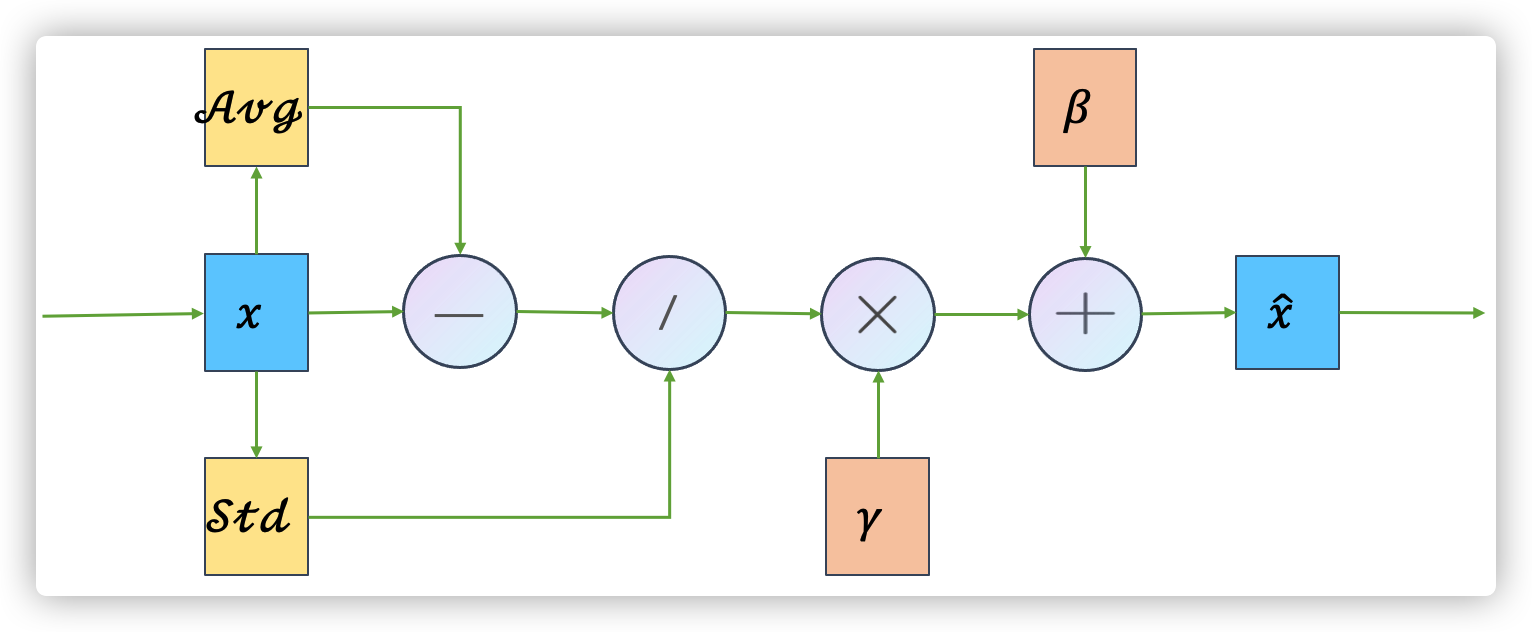
2、LN 为了解决什么问题#

深度模型训练时所需要的计算资源非常大，想要减少训练所需时间的一个方法是：normalize the activities of neurons
增加训练过程的稳定性；

3、LN 出现之前是如何解决上述问题的#

LN 出现之前通过 BN 解决上述问题；

BN的优点：

可以解决 "convariate shift" 问题，缩短了模型训练所需的时间；
能够使饱和激活函数的输入落在非饱和区，增加了训练的稳定性；

BN的缺点：

当 batch size 特别小时，表现不好；
当每条数据的长度不一致时，比如文本数据，效果不好；
在 RNN 网络中，表现不好；

4、LN 的优势#

Normalization 的作用：降低了对参数初始化的需求，允许使用更大的学习率，有一定的正则化作用可抗过拟合，使训练更加稳定。

假设某一层输出的中间结果为 $[m, T]$ ， $m$ 为batch-size， $T$ 为每条数据的特征数量，那么：

BN 是对 $m$ 这个维度做归一化；
LN 是对 $T$ 这个维度做归一化；

优势（以下都有待考证）：

在 RNN 网络中，表现较好；
在 batch size 较小的网络中，表现较好；
LN 抹杀了不同样本间的大小关系，保留了同一个样本内部的特征之间的大小关系，这对于时间序列任务或NLP任务来说非常重要；

5、LN效果测试代码#

import torch
import torch.nn as nn

# NLP例子，一般在NLP任务中，其维度为[batch_size, seq_len, hidden_dim]，LayerNorm操作仅对最后一个维度做操作
batch, sentence_length, hidden_dim = 20, 5, 10
embedding = torch.randn(batch, sentence_length, hidden_dim)

print("LayerNorm前, 均值: ")
mean_result = embedding.mean(dim=-1)  # 计算维度 hidden_dim 的均值
print([f"%.2f" % float(y) for x in mean_result.detach().numpy().tolist() for y in x][:20], "...")
print("LayerNorm前, 方差: ")
var_result = embedding.var(dim=-1)  # 计算维度 hidden_dim 的方差
print([f"%.2f" % float(y) for x in var_result.detach().numpy().tolist() for y in x][:20], "...")

# 该LayerNorm层的input的维度为[*, hidden_dim]，其仅对初始化时给定的hidden_dim这个维度做归一化
layer_norm = nn.LayerNorm(hidden_dim, elementwise_affine=False)
embedding = layer_norm(embedding)

print("LayerNorm后, 均值: ")
mean_result = embedding.mean(dim=-1)  # 计算维度 hidden_dim 的均值
print([f"%.2f" % float(y) for x in mean_result.detach().numpy().tolist() for y in x][:20], "...")
print("LayerNorm后, 方差: ")
var_result = embedding.var(dim=-1)  # 计算维度 hidden_dim 的方差
print([f"%.2f" % float(y) for x in var_result.detach().numpy().tolist() for y in x][:20], "...")

输出结果：

LayerNorm前, 均值: 
['0.23', '0.23', '0.18', '-0.06', '-0.45', '-0.24', '0.34', '0.23', '-0.47', '-0.44', '0.12', '-0.26', '-0.37', '0.33', '-0.50', '0.11', '0.14', '0.37', '-0.12', '0.31'] ...
LayerNorm前, 方差: 
['1.34', '0.51', '1.16', '0.90', '0.17', '0.50', '0.56', '0.61', '0.70', '1.06', '0.85', '1.26', '1.34', '1.45', '1.52', '0.75', '0.63', '1.37', '1.34', '1.51'] ...
LayerNorm后, 均值: 
['0.00', '-0.00', '-0.00', '0.00', '0.00', '-0.00', '0.00', '0.00', '0.00', '0.00', '0.00', '0.00', '0.00', '-0.00', '0.00', '0.00', '-0.00', '-0.00', '-0.00', '0.00'] ...
LayerNorm后, 方差: 
['1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11', '1.11'] ...

可以看出，经过归一化之后，其均值为0，方差为1.11（这里为什么是1.11，而不是1，还没搞清楚）；

6、LN实现代码#

下面是按照自己的理解实现的 LayerNorm 的代码：

import torch

class LayerNorm(torch.nn.Module):
    """
    该脚本中实现的 LayerNorm 与 pytorch 中的不太一样。pytorch 的 LayerNorm 的输入参数 normalized_shape 可以是
    整型，也可以是 list，当其为 list 时表示对输入的后 len(normalized_shape) 个维度做归一化。而在该脚本中仅会对最后
    一个维度做归一化，所以该脚本是一个简化版本。
    """

    def __init__(self, hidden_size, epsilon=None):
        super().__init__()

        self.epsilon = epsilon if epsilon is not None else 1e-12

        self.gamma = torch.nn.Parameter(torch.nn.ones(hidden_size))
        self.beta = torch.nn.Parameter(torch.nn.zeros(hidden_size))

    def reset_parameters(self):
        torch.nn.init.ones_(self.gamma)
        torch.nn.init.zeros_(self.beta)

    def forward(self, inputs):
        """
        这里假设输入inputs的维度为: [batch_size, seq_len, hidden_size]，或者是其他高维度的张量，然后直接对
        最后一个维度进行normalize。
        """

        # ------------------- 各中间变量的维度说明 -------------------
        # inputs  : [batch_size, seq_len, hidden_size]
        # avg     : [batch_size, seq_len, 1]
        # var     : [batch_size, seq_len, 1]
        # results : [batch_size, seq_len, hidden_size]
        # results_affine : [batch_size, seq_len, hidden_size]
        # --------------------------------------------------------

        avg = torch.mean(inputs, dim=-1, keepdim=True)
        var = torch.var(inputs, dim=-1, keepdim=True)
        results = (inputs - avg) / torch.sqrt(var + self.epsilon)  # 这里对 avg 和 var 的最后一个维度会进行广播
        results_affine = self.gamma * results + self.beta
        return results_affine

7、ConditionalLN实现代码#

另外 conditional layer norm 的实现代码也放在这里，原理见：

https://kexue.fm/archives/7124

import torch

class ConditionalLayerNorm(torch.nn.Module):

    def __init__(self, hidden_size, conditional_hidden_size=None, epsilon=None):
        super().__init__(self)

        self.hidden_size = hidden_size
        self.conditional_hidden_size = conditional_hidden_size
        self.epsilon = epsilon if epsilon is not None else 1e-12

        self.gamma = torch.nn.Parameter(torch.ones(hidden_size))
        self.beta = torch.nn.Parameter(torch.zeros(hidden_size))

        if self.conditional_hidden_size is not None:
            self.linear_gamma = torch.nn.Linear(conditional_hidden_size, hidden_size)
            self.linear_beta = torch.nn.Linear(conditional_hidden_size, hidden_size)

    def reset_parameter(self):
        torch.nn.init.ones_(self.gamma)
        torch.nn.init.zeors_(self.beta)

    def forward(self, inputs, condition=None):
        avg = torch.mean(inputs, dim=-1, keepdim=True)
        var = torch.var(inputs, dim=-1, keepdim=True)
        results = (inputs - avg) / torch.sqrt(var + self.epsilon)

        if self.conditional_hidden_size is not None and condition is not None:
            condition_gamma = self.linear_gamma(condition)
            condition_beta = self.linear_beta(condition)
            self.gamma = self.gamma + condition_gamma
            self.beta = self.beta + condition_beta

        results = self.gamma * results + self.beta
        return results

8、从 ConditionalLN 出发几种融合信息的方式#

融合到embedding层，这种是离散的，比如词信息、知识图谱信息等；

融合到信息传递时某个中间层，这种是连续的；

上述两种都是将新的信息融合到在模型中传递的信息流中，还有一种更特殊的是：将信息融合到模型权重中，比如 ConditionalLN。

Keys	Action
`?`	Open this help
`n`	Next page
`p`	Previous page
`s`	Search