Megatron-LM#
Megatron 这片论文中提出的张量并行(也称模型并行),主要是针对 transformer 这种模型结构所设计的。所以其会对 MLP 层和 MHA 层有不同的设计,分别描述如下。
MLP 部分#
原始公式:
\begin{equation}\begin{split}
Y &= \text{GeLU}(X \cdot A) \\
Z &= \text{Dropout}(Y \cdot B)
\end{split}\end{equation}
Tensor Parallel 的拆分过程如下图所示,将矩阵 A 拆分为 [A1, A2],将矩阵 B 拆分为 \begin{bmatrix}B1 \\ B2\end{bmatrix}:
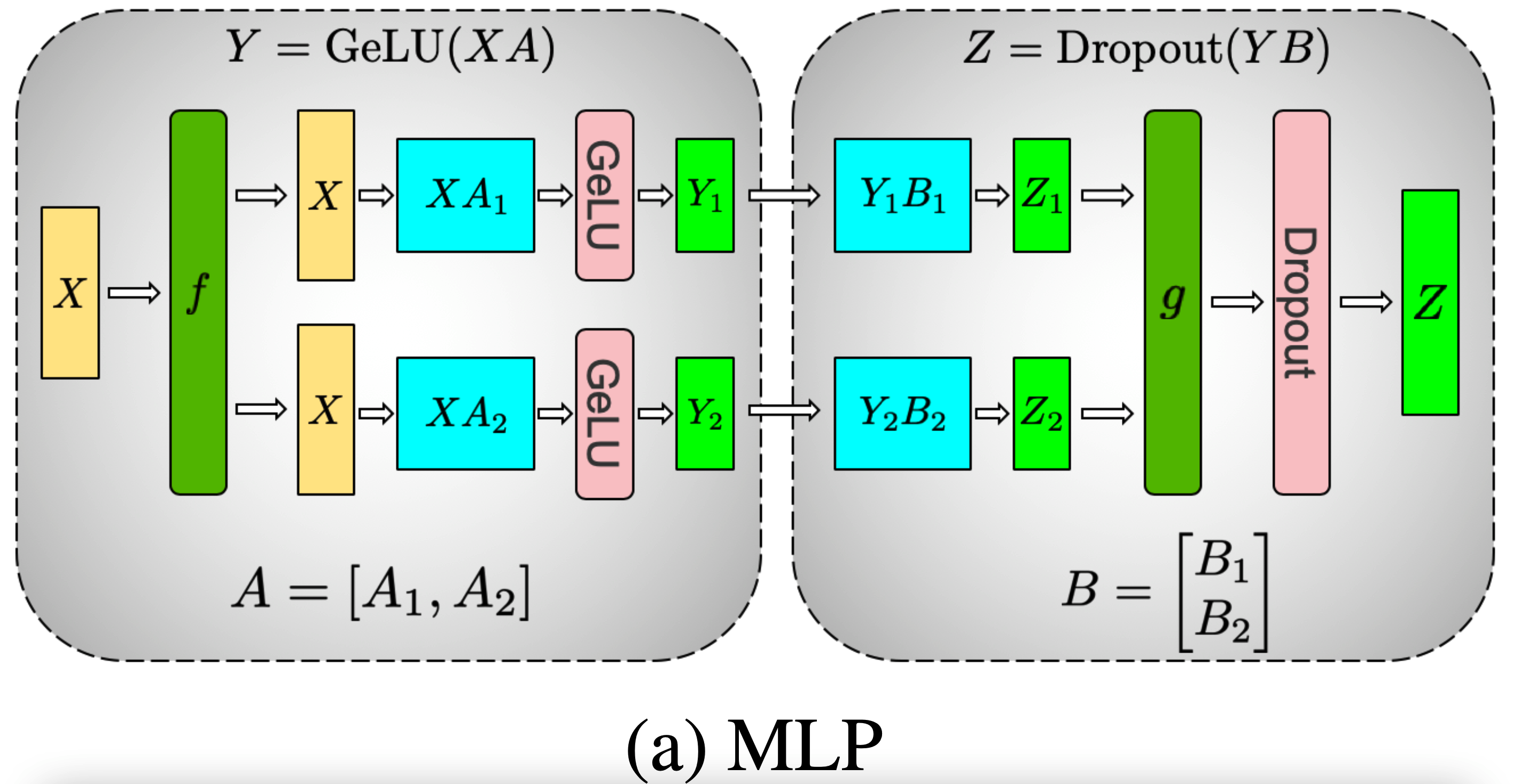
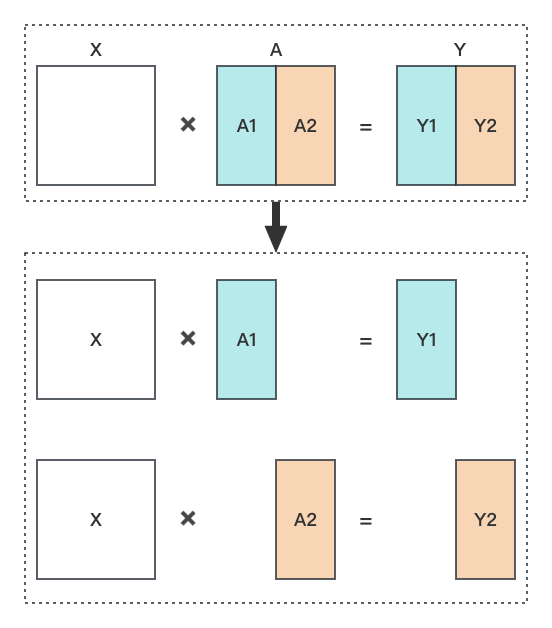
公式 Y = \text{GeLU}(X \cdot A) 拆分之后矩阵的形状如下图所示(得到 Y1 和 Y2 之后,将这两个矩阵 concat 在一起就可以得到矩阵 Y,当然实际上不会有这个 concat 操作,因为不需要得到完整的矩阵 Y):
| 图1 |
|---|
 |
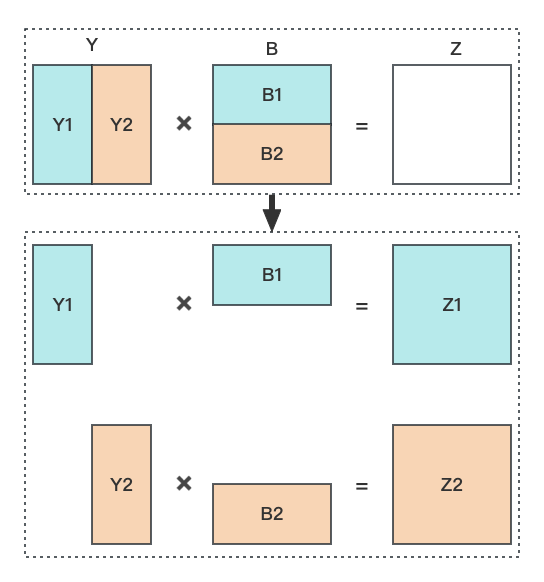
公式 Z = \text{Dropout}(Y \cdot B) 拆分之后矩阵的形状如下图所示,得到 Z1 和 Z2 之后,将这两个矩阵 逐个元素相加 之后得到矩阵 Z(矩阵 Z、Z1、Z2 的维度都是相同的):
| 图2 |
|---|
 |
上面是以两张卡为例进行介绍的,矩阵都是被划分为了两份,那么如果是有三张卡,矩阵需要被划分为三份的话,应该如何操作?并且矩阵划分为的三份的维度必须要完全一致吗?
MHA 部分#
原始公式:
\begin{equation}\begin{split}
Y &= \text{Self-Attention}(X) \\
Z &= \text{Dropout}(Y \cdot B)
\end{split}\end{equation}
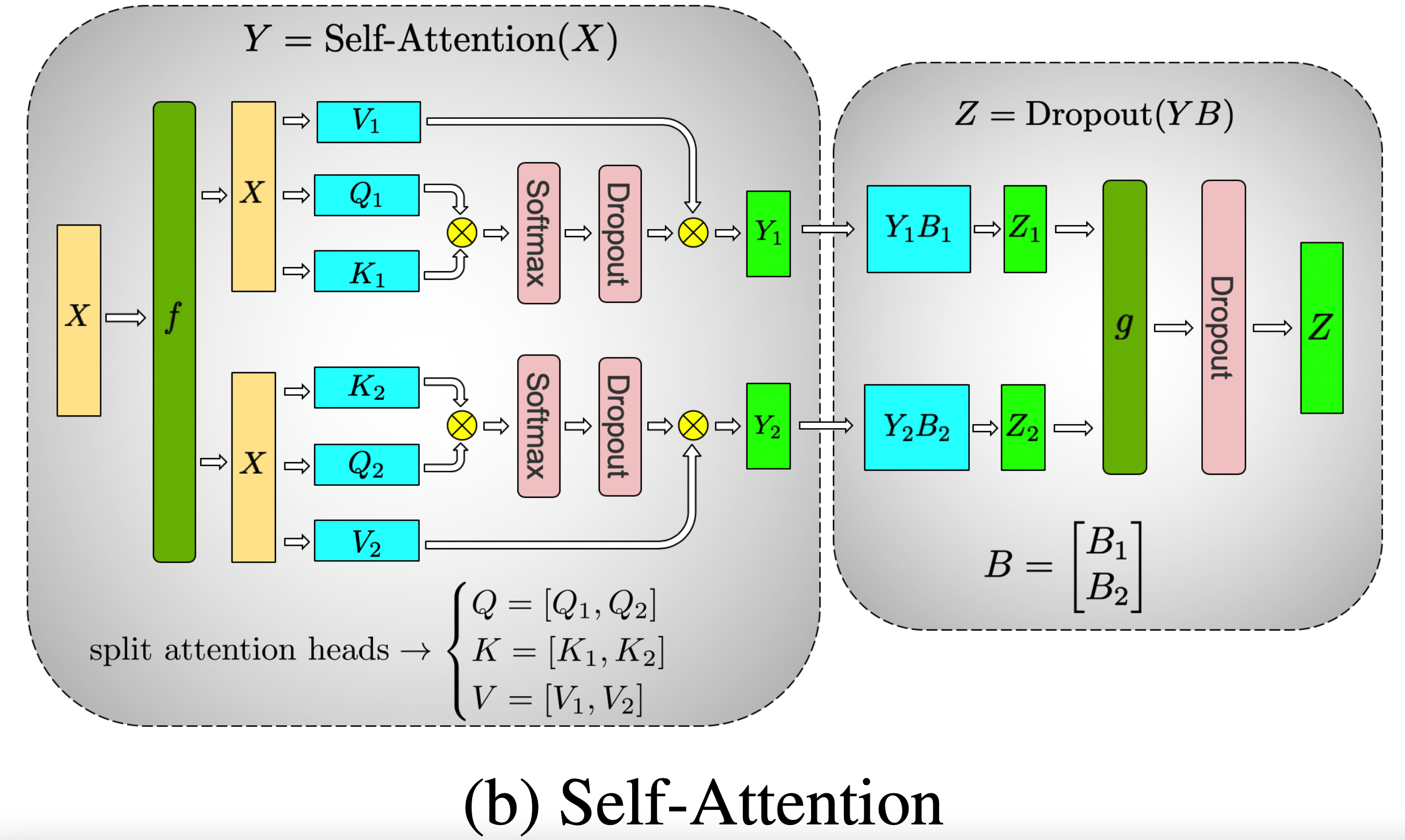
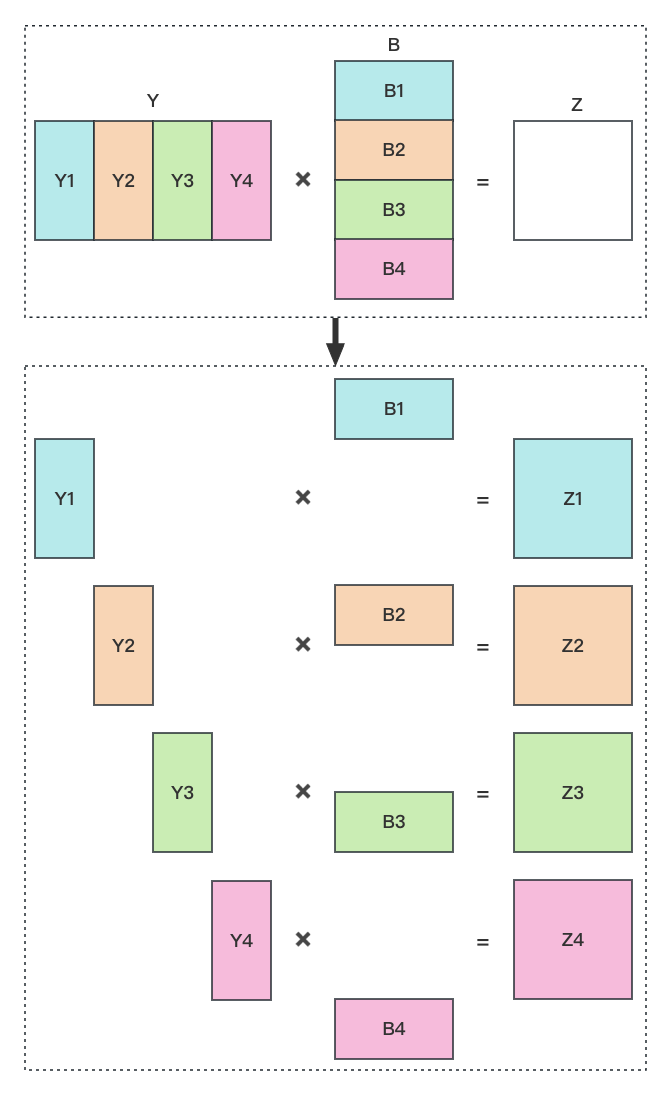
上图中的右侧部分也就是图2,如果有多个头时也是基本相同的,比如有四个头时拆分后矩阵的形状如下图所示。将矩阵 Z1、Z2、Z3、Z4 逐个元素相加起来就得到矩阵 Z。
| 图3 |
|---|
 |