[隐藏左侧目录栏][显示左侧目录栏]

从机器翻译中理解注意力(attention)机制#

参考的论文链接: https://arxiv.org/abs/1508.04025

1、背景说明#

机器翻译任务是典型的Encoder-Decoder结构。当然，虽然都是Encoder-Decoder结构，但是Encoder是输出一个向量还是输出多个向量，Encoder输出的向量是如何构建的等等，这些部分都可以有很多种设计，所以也很复杂。当然这不是本篇文章的重点，本篇文章主要目的是了解一下在self-attetion出现之前的注意力机制是怎么使用的，了解一下由最初的注意力机制到self-attention的发展过程。

由于是要了解注意力机制，所以具体采用的是RNN、LSTM、GRU还是什么别的模型结构，这里不关心，直接把其当做一个黑盒，这个黑盒的模型结构会接受两个输入，给出一个输出。

两个输入为：

  • h_{t-1}：表示前一个时间步的隐层输出；
  • x_t：表示当前时间步输入的token；

一个输出为：

  • h_t：表示当前时间步的隐层输出；

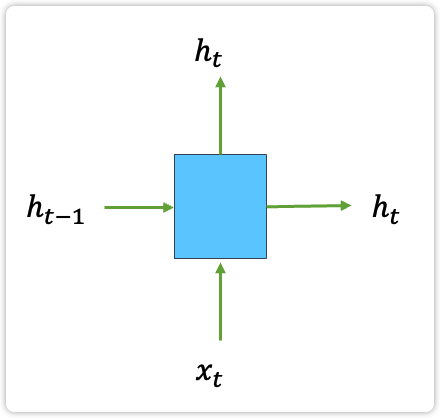
如下图所示，其中向上的箭头和向右的箭头输出内容可以是相同的，也可以是不同的，为了简化，这里选择它们两个是相同。下图中的这个模块的功能就对应图2中的蓝色或红色模块的功能。

图1: 模型中单个模块的输入输出结构

2、任务定义以及符号说明#

原始输入序列（source sentence）为： x_1, x_2, ..., x_n

目标输出序列（target sentence）为： y_1, y_2, ..., y_m

在原论文中这部分的符号使用的有点奇怪，在定义原始输入序列时使用的是符号 x ，但是在后面的推导过程中全部使用的符号 s ，这里不对其做纠正，只要知道后面的所有的 s 其实就是输入数据 x 即可。

Decoder部分解码的联合概率为下述公式，其中 s 表示原始输入序列：

\begin{equation}\log p(y|s) = \sum_{j=1}^m \log p(y_j|y_{<j}, s)\end{equation}

上述公式中的 p(y_j|y_{<j}, s) 表示每个token的解码概率，在后面涉及 attention 的部分还会进行说明。

隐藏层 h 的计算公式为下述公式，就像在第一部分中所描述的，这里的 f(\cdot) 对应着哪种模型结构在本文中并不关心，只要其输入为 h_{t-1} 和 s ，输出为 h_t 即可：

\begin{equation}h_j = f(h_{j-1}, s)\end{equation}

目标函数为下述公式，其中 D 表示训练数据集：

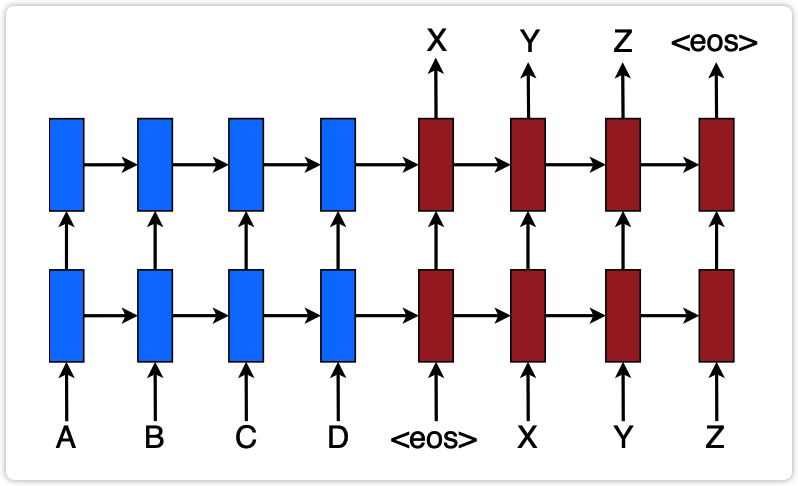
\begin{equation}J_t = \sum_{(x,y) \in D} - \log p(y|x)\end{equation}
图2: 本文中使用机器翻译模型结构示意图

3、涉及attention的模型结构#

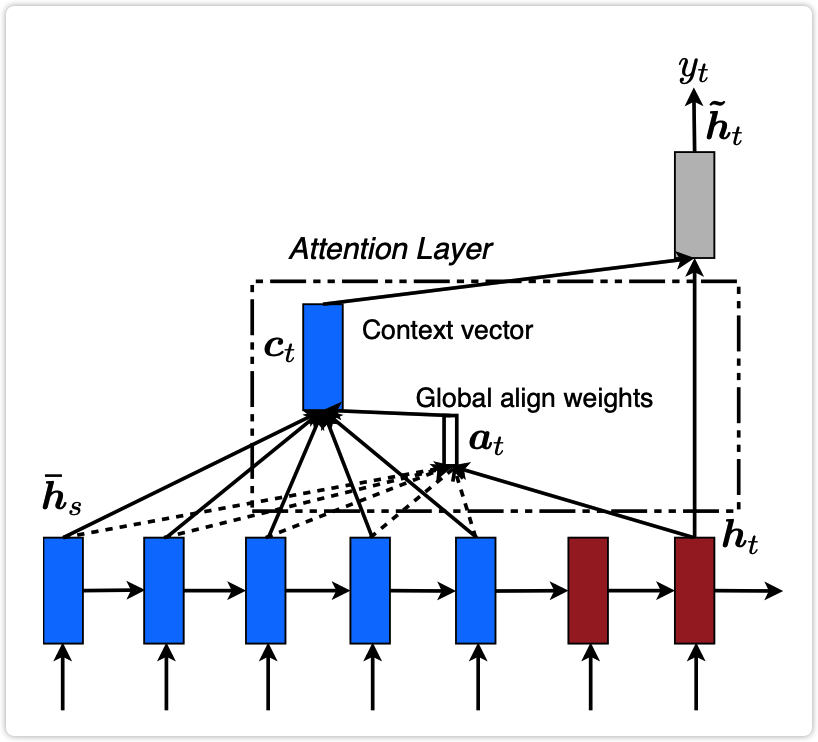
图3: LSTM网络中的注意力机制模型结构

每个token的解码概率：

\begin{equation}p(y_t|y_{<t},s) = \text{softmax}(W_s \cdot \tilde{h}_t)\end{equation}

其中 \tilde{h}_t 表示Decoder中对每个token输出的logits，公式如下，在该公式中 [c_t;h_t] 表示concat操作：

\begin{equation}\tilde{h}_t = \tanh (W_c \cdot [c_t;h_t])\end{equation}

其中 c_t 表示对原始输入序列encoder之后得到的一个向量，公式如下：

\begin{equation}c_t = \sum_{l = 1}^L a_t^{(l)} \bar{h}_s^{(l)}\end{equation}

在该公式中，L 表示原始输入序列的长度。a_t^{(l)} 表示在预测第 t 个token时，原始输入序列中第 l 个token的权重，这里的 a 就是 attention 的首字母，所以 a_t^{(l)} 就是注意力权重。\bar{h}_s^{(l)} 表示原始输入序列第 l 个token对应的隐层输出。注意这里的 a_t^{(l)} 是一个标量，而 \bar{h}_s^{(l)} 是一个向量，该公式的含义就是按照权重 a_t^{(l)} 对原始输入序列中每个token的隐向量进行加权求和得到一个新的向量 c_t。

在预测第 t 个token时的权重 a_t 的计算公式为，该公式其实就是在对原始输入序列中每个token的得分做softmax：

\begin{equation}a_t^{(l)} = \frac{\exp (\text{score}(h_t, \bar{h}_s^{(l)}))}{\sum_{l'=1}^L \exp (\text{score} (h_t, \bar{h}_s^{(l')}))} = \text{softmax}(\text{score}(h_t, \bar{h}_s))\end{equation}

这里的 \text{score}(h_t, \bar{h}_s^{(l)}) 是一个标量，具体的计算公式有多种形式，比如如下三种：

\begin{equation}\text{score}(h_t, \bar{h}_s^{(l)}) = \begin{cases} h_t^{\top} \bar{h}_s^{(l)} \\ h_t^{\top} W_a \bar{h}_s^{(l)} \\ v_a^{\top} \tanh (W_a [h_t; \bar{h}_s^{(l)}]) \end{cases}\end{equation}

4、将上述注意力机制与self-attention做一下对比#

将上述公式(7)代入到公式(6)中得到：

\begin{equation} \begin{split} c_t &= \sum_{l = 1}^L \text{softmax}(\text{score}(h_t, \bar{h}_s^{(l)})) \cdot \bar{h}_s^{(l)} \\ &= \sum_{l = 1}^L \text{softmax}(h_t^{\top} \bar{h}_s^{(l)}) \cdot \bar{h}_s^{(l)} \qquad\qquad \text{score}(h_t, \bar{h}_s^{(l)})\text{采用公式(8)中的第一个形式} \end{split}\end{equation}

然后写一下self-attention的计算公式为：

\begin{equation}\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^{\top}}{\sqrt{d_k}}) V\end{equation}

可以看出公式(9)最后的形式和self-attention已经非常相似了。

公式(9)中有一个求和符号的原因是 \text{softmax}(h_t^{\top} \bar{h}_s^{(l)}) 是一个标量，可以将这 L 个标量转化为向量的写法，那样就没有了求和符号。

另外，公式(9)中是目标输出序列中第 t 个token对原始输入序列的注意力，可以说是一个向量，元素个数为 L 。而self-attention的公式中是所有时间步的token对整个序列的注意力，这个注意力是一个矩阵。该矩阵中的单个元素 a_{ij} 的公式如下：

\begin{equation}\begin{split} a_{ij} &= \text{softmax}(\frac{q_ik_j^{\top}}{\sqrt{d_k}}) \\ &= \frac{\exp(q_ik_j^{\top})}{\sqrt{d_k}\sum_{r \in S_i} \exp(q_ik_r^{\top})} \end{split}\end{equation}