Pre Norm 与 Post Norm#
1、公式#
Post Norm 的公式:
Pre Norm 的公式:
2、实验中观察到的现象#
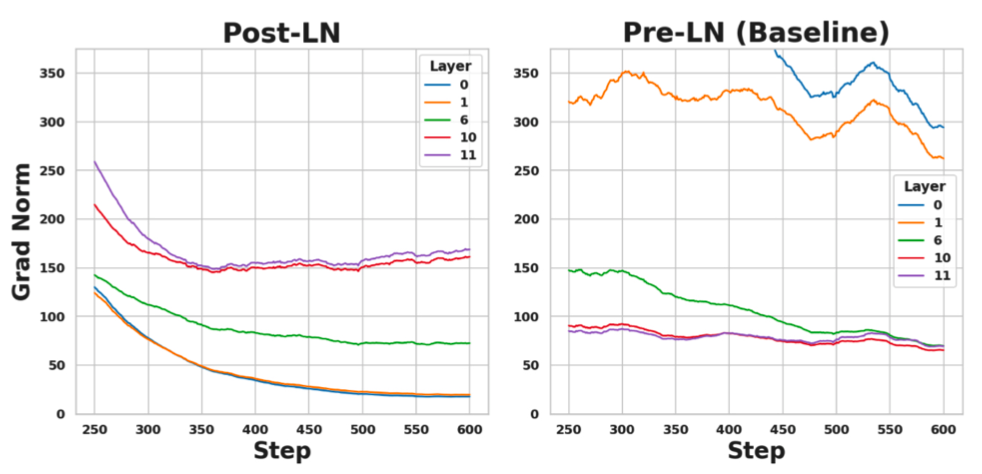
这是一个总共12层,有125M参数的模型。下图展示的是在模型训练的早期(可以看出step都是小于600的),第0层、第1层、第6层、第10层、第11层的梯度的平均L1范数值。
可以看出,使用 Post Norm 时,第0层和第1层的梯度较小,第10层和第11层的梯度较大。也就是靠前的层梯度较小,靠后的层梯度较大。并且有其他研究表明,靠前层的梯度还会随着训练的进行还会迅速减小,导致靠前的层之后就得不到充分的训练。
使用 Pre Norm 时,第0层和第1层的梯度较大,第10层和第11层的梯度较小。也就是靠前的层梯度较大,靠后的层梯度较小。
就理想情况来说,无论是"靠前层梯度小靠后层梯度大",还是"靠前层梯度大靠后层梯度小",都不是想要的,最想要的是:每一层的梯度是相同的(这里不是说梯度完全相同,而是梯度的统计值相同,比如每层梯度的L1范数值相同)。做这方面的工作有很多,比如 NormFormer 是在 Pre Norm 的基础上做优化,通过缓解 "靠前层梯度大靠后层梯度小" 的问题达到每层梯度相同;DeepNet 是在 Post Norm 的基础上做优化,通过缓解 "靠前层梯度小靠后层梯度大" 的问题达到每层梯度相同;
上述现象出自论文: NormFormer: Improved Transformer Pretraining with Extra Normalization
上面是从实验中观察到的现象,下面从理论方面分析一下产生该现象的原因。
3、残差连接与 Normalize 的联系#
残差连接这种设计的思路是给比较靠前面的层一条绿色通道,反向传播时梯度可以沿着这条绿色通道直接传递到比较靠前面的层,其前向传播的公式为:x + F(x)。
记随机变量 x 的方差为 \sigma_1^2,记随机变量 F(x) 的方差为 \sigma_2^2,并且假设这两个随机变量是相互独立的,那么有随机变量 x+F(x) 的方差为 \sigma_1^2+\sigma_2^2。
这里利用了方差的性质:如果 x、y 是独立的随机变量,那么有 \text{Var}(x+y) = \text{Var}(x) + \text{Var}(y)。
更多方差的性质见: https://zhuanlan.zhihu.com/p/161505873
可以看出,由于方差本身必然是非负的,在残差连接的结构设计下,随着层数的加深,方差是越来越大的,所以需要有一个策略控制方差在一定的范围内。而 normalize 就是能够控制方差很好的一种方法,下面分别分析 Pre Norm 和 Post Norm 在控制方差方面的效果,以及各自自身的缺陷。
4、Post Norm#
Post Norm 的公式为 x_{t+1} = \text{Norm}(x_t + F_t(x_t))
在对其分析之前,假设初始状态下 x 与 F(x) 的方差都是1,所以此时 x+F(x) 的方差为2。经过 Post Norm 之后 x+F(x) 的方差又变为了1。
也就是说对 x+F(x) 做 Norm 等同于对 x+F(x) 除以 \sqrt{2},如下公式所示:
基于上述公式,一直递归下去,公式如下所示:
上述推导出的公式的最后一行的含义为:模型的第 t+1 层的输出结果是由模型第1层的原始输入x_1、模型第1层的输出结果F_1(x_1)、模型第2层的输出结果F_2(x_2)直到模型第t层的输出结果F_t(x_t)加权求和得到的。
主要就是看这个加权中的权限值,第1层的原始输入、以及从第1层到第t层的输出结果的权重为 \Big\{\frac{1}{2^{t/2}}, \frac{1}{2^{t/2}}, \frac{1}{2^{(t-1)/2}}, ... ..., \frac{1}{2^{2/2}}, \frac{1}{2^{1/2}}\Big\}。可以明显的看出越靠前的层,其衰减的越严重。
综合来说:
- 无论模型的哪一层,经过 Post Norm 之后其方差都被严格的控制到一个固定的范围;
- Post Norm 会导致越靠前的层衰减的越严重,这和残差连接设计的初衷是相悖的。另外在实际使用中,使用了 Post Norm 之后模型训练起来也比较困难,必须要使用 warmup 等机制来保证模型收敛。
5、Pre Norm#
Pre Norm 的公式为 x_{t+1} = x_t + F_t(\text{Norm}(x_t))
基于该公式,一直递归下去,得到的公式如下所示:
由上述公式推导的最后一行可以看出,第 t+1 层模型的输出是由:第1层的原属输x_1、以及各层模型的输出直接求和得到的。相比于 Post Norm 对越靠前的层衰减越严重,这里的 Pre Norm 对待所有层的输出一视同仁,直接求和。
另外,容易看出随着层数的加深,整体的方差是在不断的增大的,所以使用 Pre Norm 时一般在最后一层之后再加个总的 Norm 层。
相比于 Post Norm,Pre Norm 能够真正的给靠前的层一个绿色通道,直达模型最终层。这样在反向传播时就不存在靠前的层梯度非常小的问题,所以 Pre Norm 训练起来要比 Post Norm 要容易训练。
每一层 F_1, F_2, ..., F_{t-1}, F_t 的输入都是经过 Norm 的,所以其输入都可看作方差为1的随机变量,而每一层的模型结构又是相同的,所以从统计上来看每一层的输出结果方差也是相同的。基于此,有一种观点认为当层数 t 比较大时,单层的输出对总输出的贡献是小量,此时有下述公式成立:
这样一个 t+2 层的网络就变成了一个更宽一些的 t+1 层的网络。由于现在整个深度学习都是使用反向传播,所以在相同的参数量下,宽而浅的网络训练起来是要比深而窄的网络要更好训练的,所以使用 Pre Norm 的网络比使用 Post Norm 的网络更好训练一些。
6、两者对比#
其实在上面的两个小节中,所以的内容都已经分析过了,这个小节只是做一下汇总。
| Pre Norm | Post Norm | |
|---|---|---|
| 好训练 | 不好训练,基本必须要和warmup一起使用 | |
| 对原始输入x和各层网络的输出一视同仁,平权相加 | 非平权,越靠前的层衰减越严重 | |
| 在对模型更新时,靠前层梯度大,靠后层的梯度小 | 在对模型更新时,靠前层梯度小,靠后层的梯度大 |